4-44-7. Felix Klein an H. Poincaré

Leipzig, den 2. Juli 1881

Geehrter Herr !

Lassen Sie mich die verschiedenen Fragen, die Sie in Ihrem willkommenen Briefe vom 27. Juni stellen, so gut es gehen will, umgehend beantworten.

1. Die Fundamentalpolygone der Kongruenzgruppen

$$\alpha\equiv\delta\equiv 1,\qquad\beta\equiv\gamma\equiv 0\pmod{n}$$

habe ich bei $n=5$ (wo durch Zusammenbiegen der Kanten das Ikosaeder entsteht) und bei $n=7$ im 14. Bande ausführlich beschrieben. Der allgemeine Fall $n=$ Primzahl bildet den Gegenstand einer Arbeit von Dyck, die eben im Druck ist. Wenn $n$ eine zusammengesetze Zahl ist, habe ich die Sache nicht erledigt.

2. „Geschlecht im Sinne der Analysis Situs“ wird jeder geschlossen Fläche beigelegt. Dasselbe ist gleich der Maximalzahl solcher in sich zurückkehrrender Schnitte der Fläche, die man ausführen kann, ohne die Fläche zu zerstücken. Wenn jetzt die betreffende Fläche als Bild der Wertsysteme $w$, $z$ einer algebraischen Gleichung $f(w,z)=0$ betrachtet werden kann, so ist ihr „Geschlecht“ eben auch das Geschlecht der Gleichung. Ihr „genre“ und mein „Geschlecht“ sind also materiell dieselben Zahlen, es liegt bei mir nur vermuthlich eine freiere Auffassung der Riemann’schen Fläche und der auf sie gegründeten Definition von $p$ zu Grunde.

3. Es gibt innerhalb der Gruppe der Modulfunktionen allerdings Untergruppen, welche ein unsymmetrisches Fundamentalpolygone besitzen, dahin gehören, wie ich in Bd. 14 nachwies, insbesondere diejenigen Untergruppen, welche den singulären Resolventen der Modulargleichung für $n=7$ und $n=11$ entsprechen.

4. Daß sich bei dem Polygon

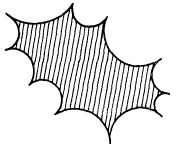
die Kreise rückwärts verlängert nicht schneiden dürfen, wenn eine eindeutige Funktion enstehen soll, ist mir in der Tat wohl bekannt. Gerade auf diesen Punkt muß man meines Erachtens die Aufmerksamkeit richten, wenn man beweisen will, daß sich die Koordinaten $w$, $z$ des Punktes einer beliebigen algebraischen Kurve als eindeutige Funktionen mit linearen Transformationen in sich angeben lassen. Ich werde Ihnen angeben, wie weit ich in dieser Frage gekommen bin. Nach den Arbeiten von Schwarz, resp. Weierstraß, kann man die Halbebene immer so auf ein Kreisbogenpolygon abbilden:

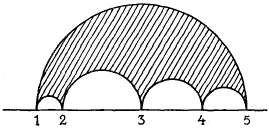
daß die Punkte I, II, III, IV, V, welche den 1, 2, 3, 4, 5 auf der Begrenzung der Halbebene entsprechen, beliebige Lage haben. Nun seien I, II, III, IV, V … die Verzweigungspunkte einer algebraischen Funktion $w(z)$; und diese algebraische Funktion möge keine anderen Verzweigungspunkte besitzen. Dann sind offenbar $w$ und $z$ eindeutige Funktionen der gewollten Art von denjenigen Hilfsvariabeln, in deren Ebene das gezeichnete Polygon liegt. Wenn also alle Verzweigungspunkte einer algebraischen Funktion $w(z)$ auf einem Kreise der z-Ebene liegen, so ist die Frage ohne weiteres zu bejahen. Wie aber, wenn das nicht der Fall ist? Da komme ich unter Umständen auf solche Polygone

wie ich sie das vorige Mal nannte. Findet keinerlei Symmetrie statt, so komme ich wenigstens (durch Aufstellung zugehöriger Differentialgleichungen des von mir behandelten Typus $\frac{\eta^{\prime\prime\prime}}{\eta^{\prime}}-\frac{3}{2}(\frac{\eta^{\prime\prime}}{\eta^{\prime}})^{2}=R(z)$) auf einen analog gestalteten Fundamentalraum, dessen Kanten unter Winkeln = Null zusammenstoßen und übrigens paarweise durch gewisse lineare Substitutionen zusammengehören. Aber ich kann nicht beweisen, daß dieser Fundamentalraum mit seinen Wiederholungen zusammen nur einen Teil der komplexen Ebene überdeckt. Und an dieser Schwierigkeit finde ich mich nun schon lange aufgehalten.

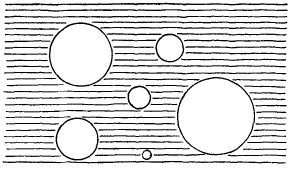
5. Übrigens bekommt man merkwürdige andere Beispiele von diskontinuierlichen Gruppen, wenn man beliebig viele einander nicht schneidende Kreise annimmt und nun an ihnen durch reziproke Radien spiegelt. Ich habe dabei den Theil der Ebene, der gleichzeitig außerhalb aller Kreise liegt, und der also das halbe Fundamentalpolygon vorstellt, der Deutlichkeit halber schraffirt. Diese Gruppen werden gelegentlich von Schottky betrachtet (Borschardts Journal t. 83, pag. 300–351), ohne daß dort ihre prinzipielle Bedeutung hervorgehoben würde.

6. Riemanns Prinzipien geben zunächst keinen Weg, um eine Funktion, deren Existenz man erschließt, wirklich zu bilden. Man ist daher geneigt, sie als unsicher zu betrachten, so gewiß es auch sein mag, daß die Resultate, welche aus ihnen folgen, richtig sind. Demgegenüber haben Weierstraß und Schwarz bei der von mir berührten Frage der Abbildung von Kreisbogenpolygonen wirkliche Bestimmungen der in Betracht kommenden Konstanten durch konvergente Prozesse gegeben. Will man Riemannsche Prinzipien gebrauchen, so kann man folgenden sehr allgemeinen Satz aufstellen. Es sei ein Polygon gegeben, mit einer oder auch mehreren getrennten Peripherien. Das Polygon kann ein mehrblättriges sein, dessen Blätter durch Verzweigungspunkte verbunden sind. Jede Peripherie besteht aus einer Anzahl von Stücken; jedes Stück gehe durch eine bestimmte lineare Substitution in eins der übrigen über. Dann kann man immer eine Funktion konstruieren, welche im Inneren des Polygons beliebige vorgeschriebene Unstetigkeiten hat, und deren reeller Teil gewisse vorgegebene Periodizitätsmoduln erhält, wenn man von einem Stücke der Begrenzung durch das Innere des Polygons zum zugehörigen Stücke übergeht. Unter diesen Funktionen sind insbesondere solche, welche im Inneren des Polygons durchweg eindeutig sind und auf je zwei entsprechenden Punkten des Randes denselben Wert aufweisen. Der Beweis läßt sich genau demjenigen nachbilden, den Riemann in § 12 des ersten Teils seiner Abelschen Funktionen für das besondere Polygon gegeben hat, das aus $p$ übereinander geschichteten Parallelogrammen besteht, die durch $2p-2$ Verzweigungspunkte verbunden sind. Dieser Satz, den ich mir übrigens erst in den letzten Tagen völlig zurechtlegte, schließt, soviel ich sehe, alle die Existenzbeweise, von denen Sie in Ihren Noten sprechen, als spezielle Fälle oder leichte Folgerungen ein. Übrigens ist mein Satz, wie manches, was ich heute schreibe, noch ungenau formuliert; ich müßte zu ausführlich sein, wenn ich das vermeiden wollte; Sie werden leicht meine Meinung erkennen.

7. Lassen Sie mich noch eine Bemerkung über eine andere Ihrer Veröffentlichungen hinzufügen. Sie sprechen davon, daß die $\theta$-Funktionen, die aus der Umkehr der algebraischen Integrale an Kurven, vom Geschlechte $p$ enstehen, nicht die allgemeinen ihrer Art sind. Daß eben diese überlegungen in Deutschland allgemein gekannt sind, können Sie nicht wissen; eine ganze Anzahl jüngerer Mathematiker arbeitet daran, die Bedingungen zu finden, durch welche sich die sogenannten Riemann’schen $\theta$-s von den allgemeinen unterscheiden. Dagegen wunderte mich, daß Sie die Konstantenzahl der Riemann’schen $\theta$ gleich $4p+2$ angeben, während es doch $3p-3$ sein muß. Haben Sie Riemann, die betr. Entwickelungen, nicht gelesen? Und ist Ihnen die ganze Diskussion, welche Brill und Nœther im 7. Bande der Math. Annalen pag. 300–307 zum Abschluß bringen, unbekannt? In der Hoffnung, bald wieder von Ihnen zu hören, bin ich

Ihr hochachtungsvoll ergebener

F. Klein

PTrL. Fricke et al. (1923, 596–599); Nörlund (1923, 106–109). See also the translations in English (§ 7-2-52) and French (§ 7-2-29).

Time-stamp: "28.04.2021 14:59"

Notes

• ¹ Dyck 1881.
• ² The two printed sources differ on the inclusion of this figure; we follow Klein’s edition, where the same figure is reproduced twice.
• ³ The remark in parentheses appears as footnote 16 in Klein’s edition of this letter, but he does not signal that it is an addition to the manuscript, unlike his other two footnotes.
• ⁴ Schottky (1877).