7-1-28. Anwendung der Integralgleichungen auf Hertzsche Wellen
Ich will heute über eine Anwendung der Integralgleichungen auf Hertzsche Wellen vortragen und insbesondere die äußerst merkwürdigen Beugungserscheinungen behandeln, welche bei der drahtlosen Telegraphie eine so wichtige Rolle spielen; ist es doch eine wunderbare Tatsache, daß die Krümmung der Erdoberfläche, welche eine Fortpflanzung des Lichtes verhindert, für die Ausbreitung der Hertzschen Wellen kein Hindernis darstellt, daß dieselben vielmehr auf der Erdoberfläche von Europa bis Amerika zu laufen vermögen. Der Umstand, daß die Hertzschen Wellen eine viel größere Länge haben als die Lichtwellen, kann allein diese Erscheinung noch nicht erklären. Eine solche Erklärung ergibt sich vielmehr erst durch Betrachtung der Differentialgleichungen des Problems.
Setzen wir die Lichtgeschwindigkeit gleich , und verstehen wir mit Maxwell
| unter | , | , | die Komponenten der magnetischen Kraft, | |
| unter | die Komponenten des Vektorpotentiales, | |||
| unter | die Komponenten der elektrischen Verschiebung, | |||
| unter | das skalare Potential, | |||
| unter | die Komponenten des Konduktionsstromes, | |||
| unter | die Dichte der Elektrizität, |
so gelten die Gleichungen
und es folgt
Wir betrachten nun eine gedämpfte synchrone Schwingung, indem wir annehmen, daß alle unsere Funktionen proportional sind mit der Exponentialgröße
Aus den so zustande kommenden komplexen Lösungen erhalten wir die physikalischen durch Trennung in reellen und imaginären Bestandteil. Der reelle Teil von gibt die Schwingungsperiode, der imaginäre die Dämpfung.
Aus unserem Ansatz folgt
und man kann daher und als retardierte Potentiale darstellen wie folgt:
ist das Raumelement im -Raume, , die Werte von , im Punkte , die Entfernung der Punkte und .
In den meisten Problemen treten zwei verschiedene Medien auf, der freie Äther und die leitenden Körper; von den letzteren wollen wir annehmen, daß sie sich wie vollkommene Leiter verhalten, daß also in ihrem Innern das Feld verschwindet, die elektrischen Kraftlinien auf ihrer Oberfläche normal stehen, während die magnetischen in dieselbe hineinfallen; dem Umstande, daß Ladung und Strömung nur an der Oberfläche des Leiters vorhanden ist, wollen wir dadurch entsprechen, daß wir die obigen Ausdrücke für und modifizieren, indem wir an Stelle der Raumintegrale Oberflächenintegrale einführen. Wir schreiben
wo , jetzt die Flächendichte der Ladung bzw. Strömung bedeuten und das Flächenelement ist.
Wir unterscheiden gewöhnlich zwei leitende Körper, der eine soll der äußere, der andere der innere Leiter heißen; sie erzeugen das “äußere” resp. das “innere” Feld; das äußere Feld ist gegeben, das innere gesucht. So ist z. B., wenn wir das Problem des Empfanges elektrischer Wellen betrachten, der Sender der äußere, der Empfangsapparat der innere Leiter; beim Probleme der Beugung elektrischer Wellen ist der Erreger der äußere, die Erdkugel der innere Leiter; bei dem Probleme der Schwingungserzeugung haben wir kein äußeres Feld, der Erreger wird dann als innerer Leiter anzusehen sein.
Um nun zum Ansatz einer Integralgleichung zu gelangen, wollen wir unter den oben erklärten Funktionen nur die zum unbekannten inneren Felde gehörigen verstehen, sodaß z.B. die obigen Integrale nur über die Oberfläche des inneren Leiters zu erstrecken sind; beachten wir nun, daß die innere Normalkomponente des elektrischen Vektors am inneren Leiter unserer obigen Annahme zufolge verschwinden muß, so folgt, wenn , , die Richtungskosinus der Normale bedeuten, aus unseren Ausgangs-Gleichungen:
wo die Normalkomponente des äußeren Feldes, also eine bekannte Funktion ist.
Bezeichnen wir jetzt die Flächendichte statt mit mit , so wird zufolge unseres Ausdruckes für
Benutzen wir ferner unseren Ausdruck für und die entsprechenden für und , so hat man
Diesen Ausdruck kann man nun in gewissen Fällen durch partielle Integrationen auf die Form
bringen, wobei eine bekannte Funktion ist. So haben wir schließlich
und dies ist die Integralgleichung 2. Art für , auf die wir hinstrebten. Im allgemeinsten Falle bekommt man zwei Integralgleichungen mit zwei Unbekannten, welche z. B. und sein mögen, wo das oben definierte ist; wir setzen , wo die Ableitung in der Normalrichtung bezeichnet und die Normalkomponente der magnetischen Kraft ist.

Die Funktion läßt sich dann besonders einfach bilden, wenn der innere Leiter ein Rotationskörper ist und das äußere Feld Rotationssymmetrie besitzt. Ist , die Bogenlänge, gemessen vom Endpunkte der Rotationsachse auf einem Meridian bis zu den Punkten , , ist ferner der Winkel zwischen der Normale in und der Meridiantangente in , so wird als Funktion von , , definiert durch die Differentialgleichung
Das Problem des Empfanges elektrischer Wellen läßt sich auf Grund der obigen Integralgleichung 2. Art behandeln.
Wollen wir nur das Problem der Erzeugung elektrischer Wellen betrachten, so haben wir das äußere Feld gleich Null zu setzen, es wird also , und wir haben eine homogene Integralgleichung vor uns; in ihr darf jedoch nicht mehr einen willkürlichen Parameterwert bedeuten, sondern ist eine zu bestimmende Zahl, die die Rolle der Eigenwerte spielt.
Ich schreibe unsere Integralgleichung in der Form
mit dem Kerne ; ich führe einen unbestimmten Parameter ein und betrachte die allgemeine Gleichung
Das erste Glied hängt von zwei Unbestimmten und ab. Wenn man die gewöhnliche Fredholmsche Methode anwendet, so erhält man die Lösung unserer obigen Integralgleichung in Gestalt einer meromorphen Funktion von , deren Nenner eine ganze Funktion von ist. Man kann nun zeigen, daß dieser Nenner auch eine ganze Funktion von wird, sodaß also auch hier unsere ausgezeichneten Werte sich als Nullstellen einer ganzen transzendenten Funktion ergeben.
Wir wollen aber jetzt das größere Problem der Beugung ausführlicher behandeln.
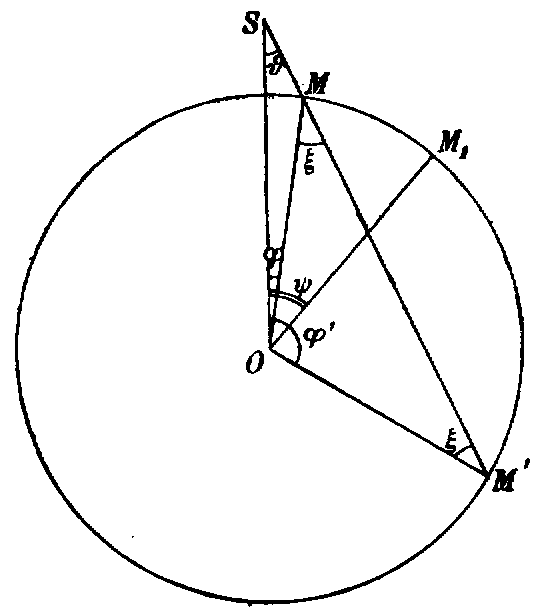
Nehmen wir zu diesem Ende an, daß der innere Leiter eine Kugel, die Erdkugel, vom Radius ist und das äußere Feld (dessen normale Komponente bedeutet) von einem punktförmigen Erreger herrührt, dessen Entfernung vom Mittelpunkt der Erde nur sehr wenig größer ist als der Radius . Wir wählen die Richtung zur -Achse und bezeichnen die Abweichung der Richtung , in der einen variablen Punkt der Kugeloberfläche bedeutet, von mit . Die Bedeutung von , , ; , ist aus der Figur ersichtlich:
Der Wert der normalen Ableitung des äußeren Feldes berechnet sich im Punkte , wie leicht zu sehen, nach der Formel
Da eine sehr große Zahl ist — denn die Länge der Hertzschen Wellen ist klein gegenüber dem Radius der Erde — genügt es meistens, in dieser Formel nur das erste Glied, das in der eckigen Klammer auftritt, beizubehalten.
Im vorhergehenden haben wir die Gleichung der Hertzsehen Wellen auf die Form
gebracht und haben gezeigt, wie der Kern berechnet werden kann. Entwickeln wir jetzt und nach Kugelfunktionen oder vielmehr, da unser Problem die Symmetrie eines Rotationskörpers mit der Achse besitzt, nach Legendreschen Polynomen , so gewinnen wir aus dieser Integralgleichung die elektrische Flächendichte gleichfalls unter der Form einer nach den Funktionen fortschreitenden Reihe. Es gilt zunächst
ist von der Form
wo eine nur von , nicht aber von abhängige Zahl ist, und eine mit der Besselschen verwandte Funktion bedeutet.
Wir verstehen nämlich unter die in der Umgebung von holomorphe Lösung der Gleichung
und sei dasjenige Integral derselben Gleichung, welches sich für große positive Werte von angenähert wie verhält. Da , von einander unabhängig sind, können wir außerdem dafür sorgen, daß
ist, wenn unter , die Ableitungen von , verstanden werden.
Die Lösung unserer Integralgleichung lautet jetzt
Da aber auch der Ausdruck von im Zähler als Faktor enthält, und sich infolgedessen dieser Term heraushebt, ist
die für die Eigenschwingungen charakteristische Gleichung.
Um zu übersichtlichen Resultaten zu gelangen, benutzen wir angenäherte Formeln. Diese beruhen darauf, daß sehr groß, andererseits aber sehr klein ist. Wir stützen uns auf die folgende Näherungsformel
, sind gegebene Funktionen von , eine sehr große Zahl, bedeutet die zweite Ableitung von , und auf der rechten Seite ist als Argument ein solcher Wert einzusetzen, für den ein Maximum oder Minimum besitzt; je nachdem der eine oder der andere Fall vorliegt, ist in dem Faktor das Zeichen oder das Zeichen zu nehmen. Hat in dem Intervall, über welches zu integrieren ist, mehrere Maxima oder Minima, so ist der Ausdruck rechts durch eine Summe analog gebildeter Terme zu ersetzen.
Durch Anwendung dieser Formel bekommen wir für die Legendreschen Polynome die folgenden, für große gültigen angenäherten Ausdrücke:
Aus ihnen folgt für die , falls ,
Dabei ist
gesetzt, und für , , , , , sind die aus der Figur zu entnehmenden Werte einzusetzen, für welche
wird. Die gleiche Näherungsformel gilt auch für , falls in der eckigen Klammer durch oder ersetzt wird; die Diskussion darüber, welches der beiden Glieder beizubehalten ist, will ich hier nicht geben.
Auch um angenähert zu berechnen, müssen wir die beiden Fälle und unterscheiden. Im ersten Falle ist
im zweiten
zu setzen. Daraus ergibt sich, daß sowohl für als auch für und große
gilt. In der Summe, durch welche wir dargestellt haben, geben demnach diejenigen Glieder, für welche nahezu ist, den Ausschlag. Für diese gilt näherungsweise
Da ferner wegen der Kleinheit von der Winkel immer nahezu bleibt, variiert als Funktion von nur sehr wenig, wenn auf die dem Werte benachbarten ganzen Zahlen beschränkt wird. Wir dürfen also, wenn wir noch die Längeneinheit so gewählt denken, daß ist, schreiben
Dabei ist der Wert der elektrischen Oberflächendichte im Punkte (s. die Figur).11endnote: 1 Der Ausdruck von , kann auch auf eine einfachere Form zurückgeführt werden, nämlich und diese Formel ist nicht eine angenäherte, sondern eine strenge.
Aus
bekommen wir
sodaß in der Nähe von der linke Ausdruck von derselben Größenordnung ist wie
Führen wir diese Annäherung in unsere Formel für ein
und ersetzen
zunächst durch , so kommen wir auf die
Reihe
Schreiben wir
so können wir
als einen Mittelwert der Reihe betrachten, und ich will durch diesen Mittelwert ersetzen. Ein solches Verfahren ist gewiß berechtigt, wenn es uns nur daran liegt, die Größenordnung von festzustellen, umsomehr als in Wirklicheit von einer Antenne nicht bloß Schwingungen einer einzigen Wellenlänge, sondern ein ganzes kontinuierliches Spektrum von Schwingungen ausgeht. Wir erhalten
und da sehr groß ist, wird dieses Integral mit
im wesentlichen übereinstimmen.
Auf ähnliche Weise zeigt man, daß der Mittelwert von
gegen den von zu vernachlässigen ist. Damit gewinnen wir das Resultat, daß von der Größenordnung
und also von der Größenordnung
ist. Die Beugung ist daher um so größer, je näher die Quelle der Erdoberfläche gelegen ist und je länger die entsendeten Wellen sind. Auf diese Weise wird die zunächst staunenerregende Tatsache verständlich, daß es mit Hilfe der in der drahtlosen Telegraphie verwendeten Hertzschen Wellen gelingt, vom europäischen Kontinent z. B. bis nach Amerika zu telegraphieren.
Wenn man nicht den mittleren Wert der Reihe betrachten will, welcher von einem Integral dargestellt wird, sondern den wirklichen Wert dieser Reihe, so hat man eine Diskussion durchzuführen, welche auf einem wohlbekannten Abelschen Satz beruht, und deren Resultate etwas komplizierter, aber sonst ganz ähnlich den vorliegenden sind.
Note. Je me suis aperçu que les dernières conclusions doivent être modifiées. Les formules approchées dont j’ai fait usage ne sont plus vraies lorsque est très voisin de . Elles doivent être alors remplacées par d’autres, où figure une transcendante entière satisfaisant à l’équation différentielle
Mais les termes qui doivent être ainsi modifiés sont en petit nombre et j’avais cru d’abord que le résultat final n’en serait pas modifié. Un examen plus approfondi m’a montré qu’il n’en est rien. La somme des termes modifiés est comparable à celle des autres termes dont j’avais tenu compte et qui est donnée par la formule précédente; il en résulte une compensation presque complète de sorte que la valeur de donnée par les formules définitives est notablement plus petite que celle qui résulterait des formules précédentes.
PD. Poincaré (1910, 23–31).
Time-stamp: “ 4.05.2019 00:49”
Literatur
- Sechs Vorträge über ausgewählte Gegenstände aus der reinen Mathematik und mathematischen Physik. Teubner, Leipzig/Berlin. link1 Cited by: 7-1-28. Anwendung der Integralgleichungen auf Hertzsche Wellen.