L’édition critique du manuscrit ‘Sur les courbes définies par une équation différentielle’ d’Henri Poincaré (1882)
Mémoire de Master 1, Épistémologie et histoire des sciences, Faculté des sciences et des techniques, Université de Nantes

Le mémoire Sur les courbes définies par une équation différentielle est un mémoire d’Henri Poincaré en quatre parties, respectivement publiées en 1881, 1882, 1885 et 1886 dans le Journal de mathématiques pures et appliquées. Je m’intéresse ici à la deuxième partie de ce mémoire à travers une édition critique du manuscrit de cette partie disponible sur le site Henri Poincaré Papers. Ainsi, afin d’introduire au mieux cette partie, il me semble nécessaire de développer le contexte mathématique dans lequel le mémoire a été écrit mais également le mémoire en lui-même, plus précisément ses deux premières parties. Pour réaliser ce travail, deux documents m’ont beaucoup aidé : la thèse de Christian Gilain de 1977, intitulée La théorie géométrique des équations différentielles de Poincaré et l’histoire de l’analyse, ainsi que son article La théorie qualitative de Poincaré et le problème de l’intégration des équations différentielles, publié en 1991, qui concentre des analyses faites dans sa thèse ainsi que l’une de ces communications au XVI^e Congrès international d’histoire des sciences en 1981, ces deux travaux étant centrés sur ce mémoire. La première section de ce travail est dédié à la mise en contexte de la deuxième partie du mémoire. Je vais donc dans un premier temps m’intéresser au contexte mathématique entourant ce dernier, en développant les travaux portant sur les équations différentielles ayant eu un impact significatif sur l’étude de ces dernières. Dans un second temps je vais me concentrer sur les travaux de Poincaré sur les équations différentielles, pour finalement dans un troisième temps introduire le mémoire dans son ensemble et décrire plus précisément sa première et sa deuxième partie.

1 L’étude des équations différentielles avant Poincaré

1.1 Cauchy, existence et unicité de la solution

Augustin Louis Cauchy (1789-1857), mathématicien français, a travaillé sur les équations différentielles, plus précisément sur l’existence et l’unicité de la solution de ces dernières. Il va notamment appliquer “la notion de limite pour transformer des schémas connus d’approximation en démonstration d’existence” (Mawhin, 1988, 233). Son travail sur l’existence de la solution est motivé par le fait qu’il n’y a que dans de rares cas où l’on peut intégrer directement une équation différentielle, et l’on utilise alors l’intégration par série. Le problème de cette méthode est d’après Cauchy que “rien ne prouvait que la série obtenue fût convergente, […] d’autre part, une série même convergente […] ne représente pas toujours la fonction dont il s’agit.” (Cauchy 1835, réed. Académie des sciences de Paris (1913, 400)). Il introduit le problème de Cauchy, qui revient à résoudre le système suivant ($y_{0}$ donné) :

$$\left.\begin{array}[]{ll}y^{\prime}(x)=f(x,y(x)),\\ y(x_{0})=y_{0}.\end{array}\right\}$$ (1)

Cauchy propose deux méthodes pour prouver l’existence de la solution d’une équation différentielle :

1°) La méthode de « Cauchy-Lipschitz » :

C’est la première méthode proposée par Cauchy en 1823 pour “prouver l’existence de la solution d’une équation différentielle” (Youschkevitch, 1981), formulée tout d’abord par Leonhard Euler (1707-1783) en 1768, puis reformulé par Rudolf Lipschitz (1832-1903) en 1868-1869. Cet méthode consiste à approcher géométriquement la courbe solution. En partant de $(1)$, on cherche à calculer une autre valeur de $y$, noté $Y$ correspondante à une autre valeur de $x$, noté $X$. Cauchy interpose alors une série de valeur entre $x_{0}$ et $X$, chaque valeur séparée de la précédente par $\Delta x$, de telle sorte que les valeurs de $y$ associés soit séparées de la précédente par $\Delta y$ (voir figure 1). De cette façon, la dernière valeur de $y$ calculée décroît vers une limite $\mathcal{F}(X)$ “fixe qui est fonction continue de $y_{0}$ et de $X$”, à condition que la différence $X-x_{0}$ ne devienne pas trop grande. Ainsi, on a $y=\mathcal{F}(X)$ est solution de (1) et se réduit à $y_{0}$ pour $x=x_{0}$. Certaines hypothèses sont nécessaires : il faut notamment que $f(x,y)$ et $\frac{\partial f(x,y)}{\partial y}$ soient continues et bornées.

Figure 1: Illustration de la méthode de Cauchy-Lipschitz
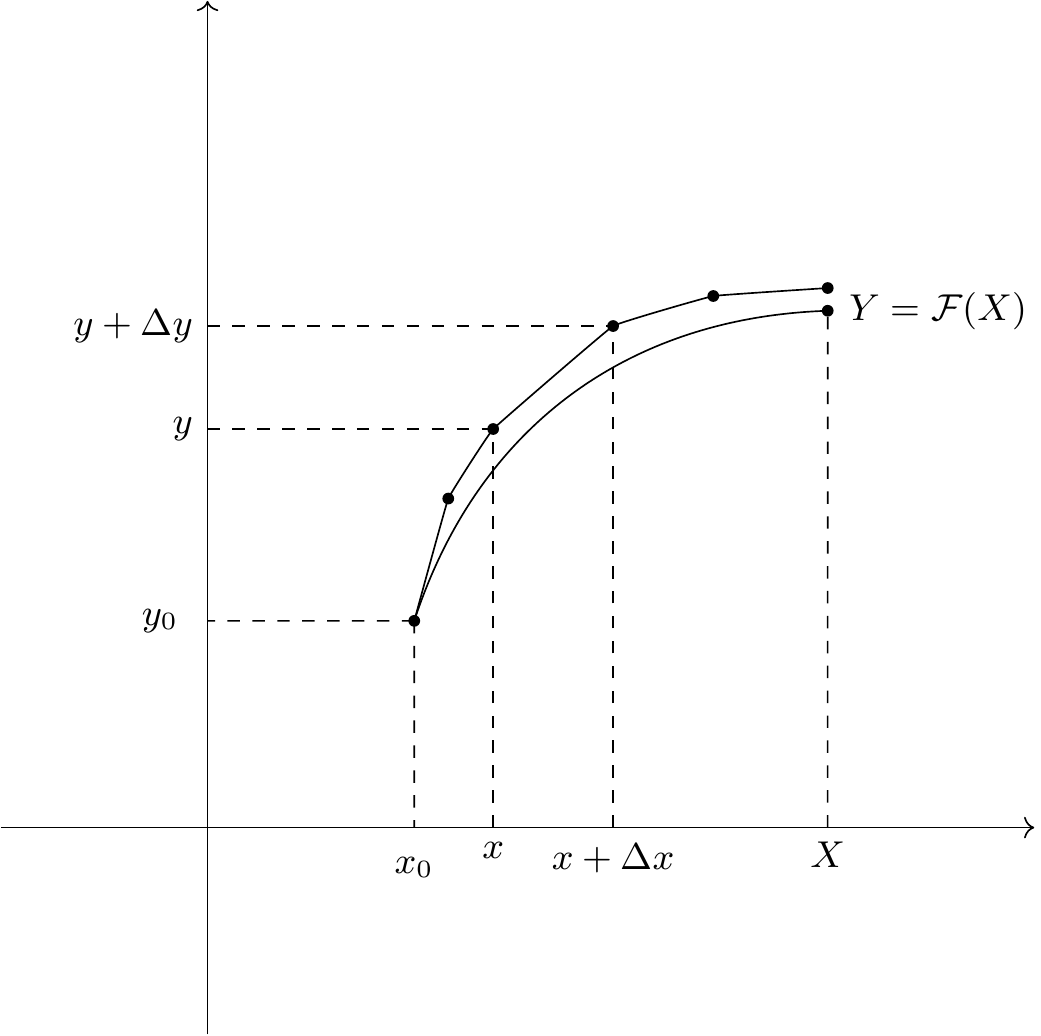
(inspiré de celle présente dans (Gilain, 1977)

2°) La méthode « des fonctions majorantes » :

Cette méthode, exposée dans le Mémoire sur l’intégration des équations différentielles se déroule en trois étapes, explicitées par Gilain (1977), et que je résume brièvement :

Étape 1 :

Cauchy affirme pour commencer que “l’intégration d’un système d’équations différentielles ordinaires du premier ordre peut se réduire à l’intégration d’une seule équation aux dérivées partielles du premier ordre, linéaire et homogène”. Ainsi soit :

$$\frac{dx}{\mathcal{X}}=\frac{dy}{\mathcal{Y}}=\frac{dz}{\mathcal{Z}}=...=\frac{dt}{\mathcal{T}}\leavevmode\nobreak\ (1)\leavevmode\nobreak\ \text{ ou }dx=\frac{\mathcal{X}}{\mathcal{T}}dt,\leavevmode\nobreak\ ...\leavevmode\nobreak\ (2)$$

on peut lui associer l’équation aux dérivées partielles :

$$\mathcal{T}\frac{\partial s}{\partial t}+\mathcal{X}\frac{\partial s}{\partial x}+\mathcal{Y}\frac{\partial s}{\partial y}+\mathcal{Z}\frac{\partial s}{\partial z}+...=0\leavevmode\nobreak\ (18)$$

On obtient alors le théorème suivant :

Deuxième théorème : - L’intégration de l’équation $(18)$ entraîne celle des équations $(2)$, et, pour obtenir l’intégrales générales de ces dernières, il suffit d’égaler à des constantes arbitraires $\xi,\leavevmode\nobreak\ \eta,\leavevmode\nobreak\ \zeta$, …les intégrales particulières $s=X,\leavevmode\nobreak\ s=Y,\leavevmode\nobreak\ s=Z$, …de l’équation $(18)$, qui ont la propriété de se réduire respectivment à $x,\leavevmode\nobreak\ y,\leavevmode\nobreak\ z$, …pour $t=\tau$.
(Académie des sciences de Paris (1913, 413), cité d’après Gilain (1977, 8))

Étape 2:

Cauchy cherche alors des solutions de l’équation $(18)$ qui satisfont les conditions du ‘deuxième théorème”, et construit des séries du type :

$$x+\nabla x+...+\nabla^{n}x+...=\xi$$

“où $\nabla$ est l’opérateur $\nabla s=-\int_{\tau}^{t}(\frac{\mathcal{X}}{\mathcal{T}}\frac{\partial s}{\partial x}+\frac{\mathcal{Y}}{\mathcal{T}}\frac{\partial s}{\partial y}+\frac{\mathcal{Z}}{\mathcal{T}}\frac{\partial s}{\partial z}+...)dt$ (donc $\nabla x=D_{t}x,\nabla^{2}x=D_{t^{2}}x,...)$.”

Étape 3 :

La dernière étape consiste à vérifier que les séries introduites sont convergentes, “du moins pour des valeurs de la différence $t-\tau$ ou $\tau-t$ suffisamment rapprochées de zéro, et comment on peut alors fixer des limites supérieurs aux erreurs que l’on commet en conservant seulement, dans chaque série les $n$ premiers termes.” (Académie des sciences de Paris (1913, 431), cité d’après Gilain (1977, 10)). Cette méthode requiert que la fonction $f$ soit analytique, c’est-à-dire développable en série entière.

Ainsi, comme l’indique Gilain, les historiens des mathématiques ainsi que les mathématiciens distinguent ces deux méthodes par leurs “différences mathématiques”, notamment dans leurs hypothèses : la première nécessite seulement que $f$ et $\frac{\partial f}{\partial y}$ soient continues et bornées, la deuxième nécessitant en plus que $f$ soit analytique.
Jean Mawhin nuance toutefois l’apport de Cauchy à la théorie des équations différentielles. En effet il précise que sa première méthode, proche de celle des polygones d’Euler, fait qu’elle se “rattache, en fin de compte, à la tradition leibnizienne” (Mawhin, 1988, 235).

Comme l’explique Gilain, “la plupart des travaux en théorie des équations différentielles générales jusqu’à Poincaré furent marqués par la domination d’une telle problématique analytique locale” (Gilain, 1977, 24), c’est-à-dire sur une résolution locale de l’équation, à travers l’utilisation de séries. Il cite plusieurs auteurs qu’il considère être dans la lignée de Cauchy, les premiers étant Charles Briot (1817-1882) et Jean-Claude Bouquet (1819-1885).

1.2 Briot et Bouquet, une étude autour des points singuliers

Les principaux travaux de Briot et Bouquet en théorie des équations différentielles sont deux mémoires publiés en 1856 : Recherches sur les propriétés des fonctions définies par des équations différentielles
(Briot and Bouquet, 1856c) et Mémoire sur l’intégration des équations différentielles au moyen des fonctions elliptiques (Briot and Bouquet, 1856b), dont je vais détailler brièvement le contenu. Un autre mémoire, intitulé Étude des fonctions d’une variable imaginaire (Briot and Bouquet, 1856a) précède les deux autres et a pour objectif d’expliciter les “principes de la théorie des fonctions d’une variable imaginaire”, ainsi que les “propriétés des fonctions définies par des séries ordonnées suivant les puissances entières et croissantes de la variable”. Tout cela dans le but final de déterminer quelles conditions sont nécessaires et suffisantes pour pouvoir développer une fonction en “série convergente suivant les puissances entières et croissantes de la variable”. Ces conditions, qui sont au nombre de trois, constituent un théorème du mémoire :

Théorème - Pour qu’une fonction soit développable en une série ordonnées suivant les puissances entières, positives et croissante de la variable, et convergente dans un cercle décrit de l’origine comme centre, il est nécessaire et il suffit que la fonction soit finie, continue, monodrome et monogène, dans ce même cercle.
(Briot and Bouquet, 1856c, 108)

Les auteurs utilisent ici les définitions de monodrome et monogène de Cauchy, une fonction est monodrome si elle “prend la même valeur au même point, quel que soit le chemin suivi pour y arriver”, et elle est monogène lorsque “la fonction admet une dérivée unique en chaque point”. Pour Gilain, ce mémoire introducteur des deux mémoires sur les équations différentielles de Briot et Bouquet montre le “rôle essentiel joué dans ces derniers par la théorie des fonctions de variable complexe”.

Le premier mémoire portant sur l’étude des équations différentielle, intitulé Recherche sur les propriétés des fonctions définies par des équations différentielles, a été présenté à l’Académie le 21 août 1854, et a été l’objet d’un rapport par Cauchy et Jacques Philippe Marie Binet (1786-1856) (Cauchy and Binet, 1855). Briot et Bouquet commence leur mémoire par ceci :

Les cas où l’on peut intégrer une équation différentielle sont extrêmement rare et doivent être regardés comme des exceptions. Mais on peut considérer une équation différentielle comme définissant une fonction, et se proposer d’étudier les propriétés de cette fonction sur l’équation différentielle elle-même.
(Briot and Bouquet, 1856c, 133)

Les auteurs expliquent ici qu’il y a dans l’étude des équations différentielles un certain intérêt à s’intéresser à la fonction définie par cette dernière, c’est-à-dire le membre de droite de l’équation $\frac{dy}{dx}=f(x,y)$, qu’ils appellent dans leur mémoire “cœfficient différentiel”. Un théorème important de ce mémoire est le théorème XVI :

Théorème XVI - Un système d’équations différentielles simultanées admettent des fonctions intégrales finies, continues, monodromes et monogènes, tant que les cœfficient différentiels restent eux-mêmes finis, continus, monodromes et monogènes.
(Briot and Bouquet, 1856c, 144)

Ce théorème d’existence et d’unicité est une amélioration de celui proposé par Cauchy, car d’après les auteurs, “Les limites de convergence données par notre méthode sont plus étendues que celles qui on été trouvées par M. Cauchy, c’est un avantage dans l’emploi des séries pour l’intégration”.
La suite du mémoire se concentre sur l’étude des cas où la fonction $f$ devient infini, puis quand elle se présente sous la forme $\frac{0}{0}$. Un résultat intéressant, relevé par Gilain, et le cas où l’équation différentielle, après changement d’inconnue et de variable, peut être écrite sous la forme :

$$\frac{dx}{dt}=\frac{ax+bt+cx^{2}+...}{t}$$

Les auteurs montrent alors que les propriétés de cette équation dépendent de la valeur de $a$, et quatre résultats sont possibles, l’équation différentielle peut alors avoir “une seule intégrale monodrome ; une intégrale monodrome et une infinité d’autres non monodromes ; aucune intégrale monodrome et une infinité de non monodromes ; une infinité d’intégrales monodromes” (Gilain, 1977, 26). Une conclusion de cet étude est faite dès le début du mémoire :

Il résulte de ce qui précède une conséquence assez remarquable, c’est qu’une fonction peut ne pas être complètement définie, lorsqu’on l’assujettit à vérifier une équation différentielle du premier ordre et à admettre une valeur initiale donné $u_{1}$ pour $z=z_{1}$. Cela arrive, en général, lorsque le cœfficient différentiel se présente sous la forme $\frac{0}{0}$ pour $z=z_{1}$ et $u=u_{1}$ ; car nous avons vu que, dans ce cas, l’équation différentielle admet, en général, plusieurs intégrales se réduisant à $u=u_{1}$ pour $z=z_{1}$. Elle en admet souvent même une infinité, et alors il s’introduit une constante arbitraire dans l’intégration, quoiqu’on donne la valeur initiale.
(Briot and Bouquet (1856c, 135), cité d’après Gilain (1977, 26))

On voit donc dans ce mémoire un intérêt de Briot et Bouquet pour les équations différentielles possédant des points singuliers, c’est-à-dire des points où la fonction $f$ (le cœfficient différentiel) n’est pas définit.

Dans leur deuxième mémoire sur les équations différentielles, intitulé Mémoire sur l’intégration des équations différentielles au moyen des fonctions elliptiques (Briot and Bouquet, 1856b), Briot et Bouquet étudient à l’aide des méthodes développées dans le mémoire précédent les propriétés des équations différentielles de la forme

$$F(\frac{du}{dz},u)=0,$$

où F est “polynôme entier entre la fonction $u$ et sa dérivée $\frac{du}{dz}$, du degré $m$ par rapport à cette dernière, et ne contenant pas la variable $z$” (Briot and Bouquet, 1856b, 199). Dans ce mémoire, les auteurs se concentrent sur les équations différentielles admettant des intégrales monodromes, où ils en déduisent alors que cet intégrale est “ou une fraction rationnelle, ou une fonction monodrome simplement périodique, ou une fonction monodrome doublement périodique”. Pour Briot et Bouquet, l’intérêt d’étudier directement l’équation différentielle est que cela nous renseigne sur les “propriétés fondamentales de la fonction intégrale, et en caractérise la nature”.

On voit ici que Briot et Bouquet ont participé activement à l’essor de l’étude des équations différentielles, en améliorant le théorème d’existence et d’unicité de Cauchy, mais également en s’intéressant aux points singuliers de ces équations.

Un autre auteur ayant une approche similaire à Briot et Bouquet, et également cité par Gilain est Charles Méray (1835,1911). En effet, dans son Nouveau précis d’Analyse infinitésimale (Méray, 1872), la forme de son théorème d’existence de solutions pour un système d’équations différentielles est d’après Gilain inspirée de celle du travail de Briot et Bouquet. Pour Méray, il faut restreindre la recherche des fonctions solutions aux fonctions olotropes, c’est-à-dire holomorphes ou analytiques, car “la condition pour certaines fonctions, de satisfaire à des équations différentielles, exige qu’elles aient des dérivées, ce qui, d’après nous, n’a de sens que pour des fonctions olotropes” (Méray, 1872, 138), cité d’après Gilain (1977, 29).

1.3 Weierstrass et le prolongement analytique

Karl Weierstrass (1815-1897) a également contribué au développement de l’étude des équations différentielles. En 1842, il propose, probablement indépendamment de celui de Cauchy, un théorème d’existence de solution pour un système d’équations différentielles de la forme :

$$\frac{dx_{1}}{dt}=G_{1}(x_{1},\dots,x_{n}),\dots,\frac{dx_{n}}{dt}=G_{n}(x_{1},\dots,x_{n}),$$

où $G_{1},\dots,G_{n}$ sont des fonctions rationnelles en $x_{1},\dots,x_{n}$. Les solutions $x_{i}(t)$ de ce système pour les conditions initiales $a_{i}$ sont sous la forme de séries entières notées $\beta_{i}(t)$, et Weierstrass détermine leur convergence à l’aide de séries majorantes.

Un autre de ses apports à la théorie des équations différentielles est celui du prolongement analytique, qui permet d’étendre le domaine de convergence d’une série. Pour ce faire, on suppose tout d’abord qu’une série est convergente à l’intérieur $T_{0}$ d’un cercle de centre $t_{0}$ et de rayon $\rho_{0}$. On prend alors un point $t_{1}$ appartenant à $T_{0}$, la série, qui était alors écrite suivant des puissances de $(t-t_{0})$, peut alors être réécrite suivant des puissances de $(t-t_{1})$, et la nouvelle série obtenue est alors convergente à l’intérieur d’un cercle $T_{1}$ de centre $t_{1}$ et de rayon $\rho_{1}$ (voir figure 2). Si $T_{1}$ est inclus dans $T_{0}$, alors $t_{1}$ correspond à un point singulier de $T_{0}$ se situant sur la frontière de ce dernier. Sinon, la nouvelle série obtenues permet alors de “calculer la fonction définie par la première en des points où cette première série est divergente” (Gilain, 1977, 28). Comme nos deux séries sont les mêmes sur l’intersection des cercles $T_{0}$ et $T_{1}$, on a donc prolonger analytiquement la fonction qui est définie par la première série.

Figure 2: Illustration du prolongement analytique de Weierstrass

Néanmoins, Gilain précise que cette méthode est “essentiellement théorique”, et ne “peut constituer l’étude globale de la solution”, limite notamment souligné par Camille Jordan (1838-1922) et Pierre Boutroux (1880-1922).

1.4 L’étude des fonctions de variable réelle

Tous les travaux présentés jusqu’ici se concentrent sur les fonctions de variables complexes, pratique qui domine alors l’étude des équations différentielles. Il existe cependant une exception à cette règle, un article de Rudolf Lipschitz (1832-1903), publié en 1876 et intitulé Sur la possibilité d’intégrer complètement un système donné d’équations différentielles (Lipschitz, 1876). Dans cette article, Lipschitz propose une démonstration de l’existence d’une solution d’une équation ou d’un système d’équations différentielles similaire à la première méthode de Cauchy présentée précédemment. Dans cette démonstration, la fonction $f(x,y)$ doit vérifier une condition correspondante à ce qu’on désigne aujourd’hui comme la “condition de Lipschitz” par rapport à $y$, cette condition impliquant que $f$ doit être localement lipschitzienne par rapport à $y$. Dans cette démonstration les variables $x$ et $y$ sont alors considérées réelles. Ainsi, dès l’introduction de son article, Lipschitz explique que la plupart des travaux portant sur la théorie des équations différentielles ont considéré des fonctions de variables complexes, en cela que “toute fonctions d’une quantité imaginaire pouvant, à l’exception de certains points du champ (Gebiet) de cette fonction, être développée en une série procédant suivant les puissances entières et positives d’une fonction linéaire de cette quantité imaginaires” (Lipschitz, 1876, 1). Lipschitz a lui pour objectif de s’intéresser aux équations différentielles dont les variables sont réelles, et où le développement en série entière n’est pas tout le temps possible. Il précise également qu’aucun travaux ne se sont déjà intéressé à cette question, une note de l’auteur précisant que Lipschitz n’avait pas connaissance des travaux effectués par Cauchy.

1.5 Conclusion

Ainsi, d’après Gilain, on voit à travers les travaux présentés précédemment, “la domination en théorie des équations différentielles ordinaires d’une problématique caractérisée notamment par un rapport privilégié avec la théorie des fonctions de variable complexe et une étude essentiellement locale des solutions des équations différentielles générales” (Gilain, 1977, 35), et rares sont les travaux s’éloignant de cette domination (par exemple les travaux de Lipschitz). Le mémoire de Poincaré, développant une théorie géométrique des équations différentielles, tranche alors avec cette domination, mais avant de développer plus en détails ce mémoire, intéressons-nous d’abord aux différents travaux de Poincaré sur l’étude des équations différentielles.

2 Les travaux de Poincaré sur les équations différentielles

Poincaré a, au début de sa carrière, contribué de manière importante à la théorie des équations différentielles, notamment sur la période 1878–1881. Christian Gilain, dans son article La théorie qualitative et le problème de l’intégration des équations différentielles (1991), distingue plusieurs types de travaux :

2.1 Étude analytique et locale des équations différentielles générales

Le premier travail de Poincaré sur les équations différentielles est une Note sur les propriétés des fonctions définies par les équations différentielles, publiée en 1878 dans le Journal de l’École polytechnique (Poincaré, 1878). Dans cette note, Poincaré rappelle des résultats de Briot et Bouquet quand le cœfficient différentiel est une fonction holomorphe. Poincaré complète alors leurs résultats, notamment en développant en série “certaines intégrales non holomorphes” (Gilain, 1991), ainsi qu’en s’intéressant aux points singuliers.
En effet, comme l’indique Georges David Birkhoff (1884-1944), dans son article The Work of Poincaré on Differential Equations de 1934, “l’application des théorèmes d’existence habituels pour un système différentiel ordinaire d’ordre 1 comme

$$\frac{dx_{1}}{X_{1}(x_{1},\dots,x_{n})}=\dots=\frac{dx_{n}}{X_{n}(x_{1},\dots,x_{n})}=\frac{dt}{1}$$ (2)

échoue aux voisinages des points singuliers $(x_{1},\dots,x_{n})$ auxquels les fonctions $X_{i}$ disparaissent”. Birkhoff rappelle alors l’intérêt de Briot et Bouquet pour l’étude de ces points singuliers, et que leurs travaux ont permis de mettre en évidence l’importance des intégrales de la forme $\psi e^{-\lambda t}=\text{const.}$, avec “$\psi$ une série entière convergente en $x_{1},\dots,x_{n}$ sans termes constants, pourvu que le point singulier en question soit pris à l’origine des coordonnées”, qui satisfont l’équation aux dérivées partielles linéaire suivante :

$$X_{1}\frac{\partial\psi}{\partial x_{1}}+\dots+X_{n}\frac{\partial\psi}{\partial x_{n}}-\lambda\psi=0$$

Birkhoff indique alors que Poincaré utilisa cette équation afin de construire les bases d’une théorie permettant de trouver les solutions autour de ces points singuliers, ce qu’il développera dans sa thèse de 1879, intitulée Sur les propriétés des fonctions définies par les équations aux différences partiel. Un de ses résultats intéressant est mentionné par Birkhoff :

Si par une transformation linéaire adéquate des variables $x_{1},\dots,x_{n}$ on peut réduire les fonctions $X_{i}$ à la forme $\lambda_{i}x_{i}+$ des termes de degré supérieur en $x_{1},\dots,x_{n}$ avec $\lambda_{i}\neq\lambda_{j}$ pour $i\neq j$ (cas général), et si il y a une ligne du plan complexe tel que les points $\lambda_{i}$ tombent d’un côté, tandis que l’origine $\lambda=0$ tombe de l’autre, alors les séries formelles sont convergentes, et l’intégrale générale de (2) proche du point singulier est fourni par les $n$ équations $\psi_{i}=ce^{\lambda_{i}t}$, ($i=1,\dots,n)$.
(Birkhoff, 1934, 1)

On peut voir dans les premiers travaux de Poincaré sur la théorie des équations différentielles, une continuité avec les travaux présentés précédémment, en cela qu’il s’inscrit dans la tradition de l’étude locale (plus précisément autour des points singuliers) ainsi que de l’utilisation de variables complexes dans son étude.

2.2 L’étude qualitative des équations différentielles

Cette étude commence avec le mémoire présenté le 22 mars 1880 à l’Académie des Sciences, mémoire qui sera plus tard retiré et correspondra aux deux premières parties du mémoire Sur les courbes définies par une équations différentielles. Poincaré se concentre ici sur les propriétés qualitatives globales des intégrales des équations différentielles ayant des variables réelles. Je détaillerais plus tard le contenu de ce mémoire, sa deuxième partie étant l’objet de cette édition critique, mais on peut tout de même noter que cette étude tranche avec les précédents travaux effectués en théorie des équations différentielles, qui comme je l’ai expliqué dans la section précédente, se concentraient sur une étude locale de ces équations ainsi qu’à leurs propriétés quantitatives (trouver la solution numérique de l’équation à travers les séries entières par exemple), tout cela dans le domaine complexe.

2.3 L’influence de Fuchs sur les travaux de Poincaré

Lazarus Fuchs (1833-1902) est un mathématicien allemand, dont les travaux portent principalement sur la théorie des équations différentielles. Il considérait que “la principale tâche était de trouver les propriétés de la solution d’une équation différentielle en tout point du plan, en particulier, où la fonction était discontinue ou multivaluée” (Gray, 1984, 3). Il a dans un premier temps considéré les équations différentielles linéaires ordinaires d’ordre $n$ de la forme

$$\frac{d^{n}y}{dx^{n}}=p_{1}\frac{d^{n-1}y}{dx^{n-1}}+\dots+p^{n}y,$$

où $p_{i}$ sont des fonctions rationnelles possédant un nombre fini de pôles (c’est-à-dire de points singuliers). Il trouve notamment que “les points singuliers des solutions doivent être parmis les points singuliers des cœfficients, et donc, en particulier, qu’ils sont fixes” (Gray, 1984, 4). Cependant, Fuchs ne s’intéresse alors qu’aux “bonnes singularités’, c’est-à-dire les pôles finis et les points de branchement logarithmiques. Poincaré continuera cette étude des solutions autour des points singuliers mais en étudiant également les points singuliers irréguliers, on retrouve ce travail dans la première partie du mémoire qu’il soumet au grand prix des sciences mathématiques de l’Académie des Sciences en juin 1880, dont il arrivera deuxième.

Dans une série de travaux publiés en 1880 et 1881, Fuchs s’intéresse ensuite plus particulièrement aux équations différentielles de la forme :

$$\frac{d^{2}y}{dz^{2}}+P(z)\frac{dy}{dz}+Q(z)y=0,$$

“où $P$ et $Q$ sont des fonctions rationnelles de la variable complexe $z$” (Gray and Walter, 1997b, 3). Fuchs, en posant $f_{1}$ et $f_{2}$ des solutions linéairement indépendantes de cette équation, considère alors

$$\int_{\zeta_{1}}^{z_{1}}f_{1}(z)dz+\int_{\zeta_{2}}^{z_{2}}f_{1}(z)dz=u_{1}(z_{1},z_{2}),$$

$$\int_{\zeta_{1}}^{z_{1}}f_{2}(z)dz+\int_{\zeta_{2}}^{z_{2}}f_{2}(z)dz=u_{1}(z_{1},z_{2}),$$

et cherche alors des propriétés de $z_{1}$ et $z_{2}$ en tant que fonction de $u_{1}$ et $u_{2}$. Cette recherche peut être vu comme une généralisation du problème d’inversion de Jacobi. Malgré les huit papiers que Fuchs a écrit sur ce sujet (Gray, 1984, 12), son étude n’a pas eu un grand succès, et Poincaré, dans son mémoire pour le grand prix de 1880, décrira l’analyse de Fuchs au cas par cas comme “confusante” et “incomplète”. Poincaré s’intéressera un peu plus tard aux équations différentielles hypergéométriques, où il découvrira l’existence ainsi que les différentes propriétés d’un nouveau type de fonctions qu’il appellera fuchsiennes.

2.4 Conclusion

On peut observer, à travers ce rapide résumé des différents travaux de Poincaré en théorie des équations différentielles, une diversité dans la manière d’étudier ces équations, au départ de manière “classique”, c’est-à-dire une étude locale (autour des points singuliers) d’équations à variable complexe, où il s’inscrit alors dans cette domination de ce type d’étude, puis, à travers son mémoire Sur les courbes définies par une équation différentielle, il souhaite opérer un changement dans la manière d’étudier les équations différentielles, ce que nous allons voir dans la prochaine partie. Finalement, il continue également d’étudier les équations différentielles à variable complexe, notamment à l’aide d’un nouvel outil qu’il a découvert : les fonctions fuchsiennes.

3 Sur les courbes définies par une équations différentielle

Le Mémoire sur les courbes définies par une équation différentielle est donc en quatre parties, publiées en 1881, 1882, 1885, 1886 dans le Journal de Mathématique pure et appliquées. Néanmoins, il devait à l’origine en être autrement. En effet, le 22 mars 1880, Poincaré soumet à l’Académie des sciences de Paris un mémoire intitulé Sur les courbes définies par une équation différentielle, mais il fera la demande de le retirer le 11 juin avant que la commission choisie pour l’étudier ne présente son rapport (Gilain, 1991, 216). D’après une note publiée aux CRAS (Comptes rendus de l’Académie des sciences), contenant un résumé du mémoire, il s’agissait des deux premières parties. L’objectif de cette section est de brièvement résumer la première et la deuxième partie de ce mémoire, en rappelant les principaux résultats développés par Poincaré.

3.1 La problématique du mémoire

Henri Poincaré, dans l’introduction de la première partie de son Mémoire sur les courbes définies par une équations différentielle (1881) explique en quoi “Une théorie complète des fonctions définies par les équations différentielles serait d’une grande utilité dans un grand nombre de question de Mathématiques pures ou de Mécanique” (p. 375), mais le problème d’une telle théorie est que seulement une petite partie des équations différentielles est intégrables, or, comme je l’ai développé précédemment, la plupart des études faites à l’époque se font à travers le calcul des solutions de l’équation. Il indique ensuite qu’une première étape a été franchi “en étudiant la fonction proposée dans le voisinage d’un des points du plan” (p. 375), mais qu’il faut désormais étendre cette analyse à “toute l’étendue du plan”. On a donc, dès le début de ce mémoire, une première ambition de Poincaré : passer de l’étude locale des équations différentielles à l’étude globale de ces dernières. Pour Poincaré, l’analyse complète d’une fonction comprend deux parties :
1°) La “Partie qualitative […], ou étude géométrique de la courbe définie par la fonction”
2°) La “Partie quantitative, calcul numérique des valeurs de la fonction”
Il fait ensuite le parallèle avec l’étude d’une équation algébrique, où l’on calcule d’abord le nombre des racines réelles (la partie qualitative) pour seulement ensuite calculer ses racines (la partie quantitative). Ici, dans le cas des équations différentielles, la partie qualitative consiste à “construire les courbes définies par des équations différentielles”. La construction et l’étude de ces courbes a pour Poincaré “un intérêt de premier ordre”, par exemple dans le cas de la mécanique céleste, où l’on peut connaître le comportement de corps céleste (s’ils se rapprochent, s’ils restent “dans une certaine région du ciel” ou s’ils s’éloigneront indéfiniment). Poincaré décrit ainsi l’analyse qualitative des équations différentielles comme un nouveau domaine s’ouvrant “devant les géomètres”, dont il veut en “franchir les frontières” en s’intéressant seulement à l’étude des équations différentielles du premier ordre. Ainsi, le commencement de l’étude d’une équation différentielle par son étude qualitative est motivée par deux raisons :
1°) Elle est la première étape de l’étude complète de cette équation, et est utile pour “le calcul numérique de la fonction”, c’est-à-dire l’étude quantitative de l’équation.
2°) Elle possède un intérêt en elle-même, car permet d’étudier le comportement des courbes définies par une équation différentielle.
Hadamard, dans son article The Early Scientific Work of Henri Poincaré, note que l’exemple de l’étude des équations algébriques est une preuve “quant au fait que l’ordre entre les deux parties (qualitative et quantitative) de l’étude, qui était habituel aux géomètres pour les questions élémentaires, doit être inversé quand on étudie des sujets plus complexes” (Hadamard, 1922, 170)

Poincaré souhaite donc faire prendre à l’étude des équations différentielles une nouvelle voie, décrite par Hadamard comme “presque complètement délaissé et comme ignoré par les prédécesseurs de Poincaré” (Hadamard, 1921, 241). Néanmoins, différentes approches qualitative ont précédé celle de Poincaré, Hadamard cite en effet comme exemple la preuve par Dirichlet du théorème de stabilité d’un équilibre, ainsi que les travaux de Sturm et et de Liouville, respectivement sur les équations linéaires et les invariants intégraux, mais cet étude qualitative est tout de même très rare. Une des principale raison avancée par Hadamard pour expliquer cette rareté est l’attirance des géomètres pour la “magnifique théorie des fonctions analytiques” (Hadamard, 1922, 171), indiquant que les géomètres ont découvert que “la plus courte voie entre deux vérités dans le domaine réel passe très souvent par le domaine complexe”

En conclusion de son introduction, il explique le cadre mathématique dans lequel il va effectuer son étude. Le point centrale de son mémoire est les courbes définies par une équation de la forme :

$$\frac{dx}{X}=\frac{dy}{Y},$$

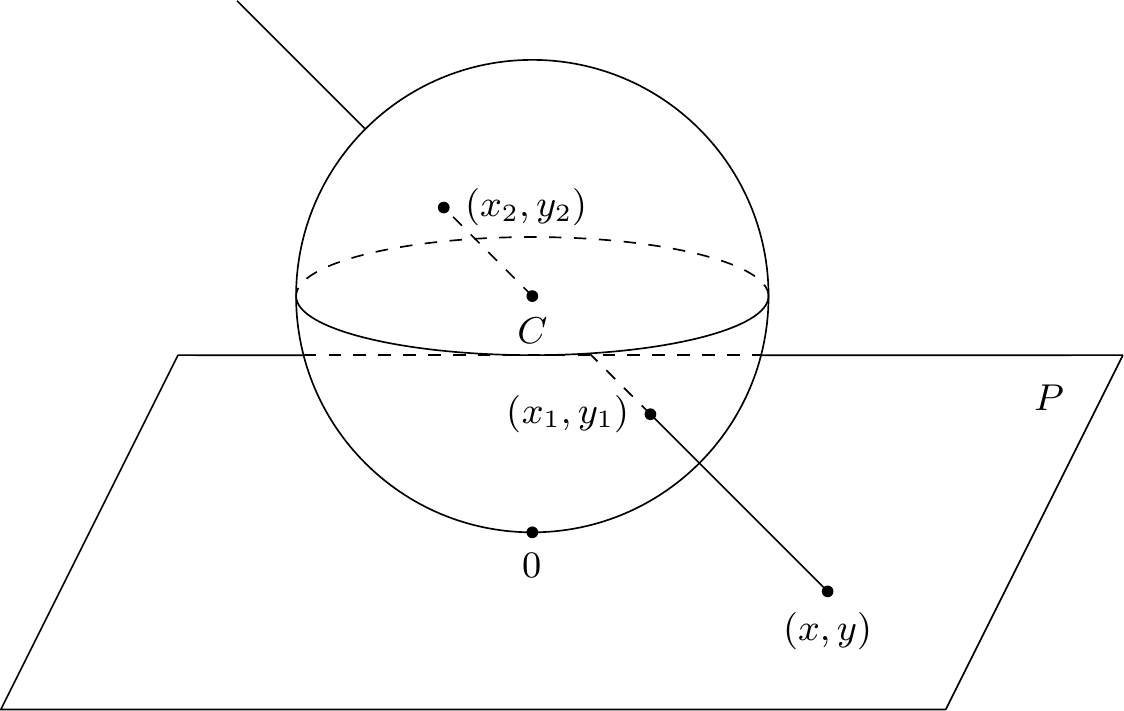
où $X$ et $Y$ sont deux polynômes entiers en $x$ et en $y$. Il appelle ces courbes des caractéristiques. Pour éviter l’étude de ses caractéristiques à l’infini, il les projette gnomoniquement sur une sphère, dont il explique le procédé (voir figure 3) :

Soient un plan $P$, et un point quelconque $(x,y)$ dans ce plan ; si l’on considère une sphère quelconque divisée en deux hémisphères par un plan parallèle au plan $P$ et que nous appellerons plan de l’équateur ; si l’on joint le centre de la sphère au point $(x,y)$, la droite ainsi déterminée, coupera la sphère en deux points diamétralement opposés ; nous appellerons $(x,y,1)$ celui qui est situé dans le premier hémisphère, $(x,y,2)$ celui qui est situé dans le second hémisphère.
(Poincaré, 1881, 378)

Figure 3: Illustration de la projection gnomonique (le centre de la sphère est $C$)

3.2 La première partie du mémoire

Je vais, dans cette sous-section, développer les différentes notions développés par Poincaré dans la première partie du mémoire publié en 1881, afin de pouvoir comprendre au mieux la deuxième partie de ce dernier.

3.2.1 Chapitre 1 : Définitions et généralités

Le premier chapitre de ce mémoire, intitulé Définitions et généralités, est composé d’un certain nombre de définitions et de théorèmes, qui d’après Poincaré, “seront d’un grand secours dans l’étude qualitative des courbes sphériques” (Poincaré, 1881, 378). Afin de mieux comprendre ces définitions, certaines seront accompagnées d’illustrations dans le plan et non sur la sphère, pour des soucis de visibilité.

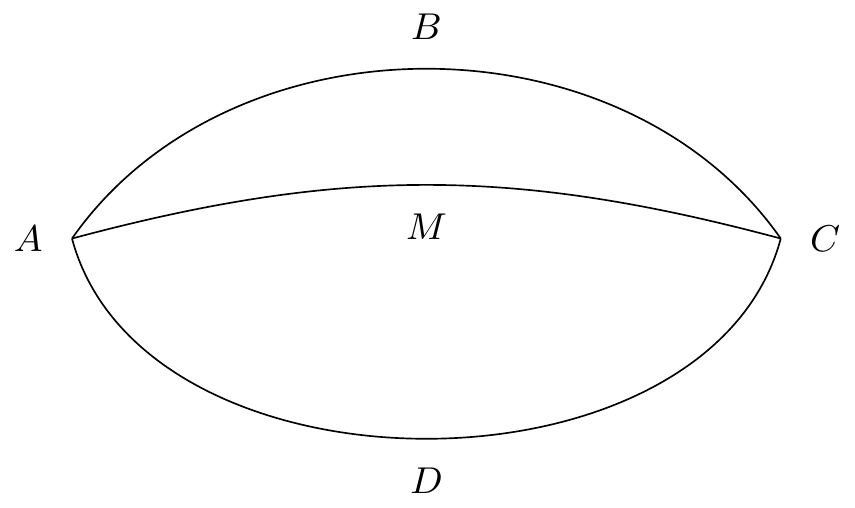
Les premières définitions concernent plus particulièrement les courbes sphériques toutes simples, ne présentant “ni point double” (c’est-à-dire que la courbe ne passe par un point qu’au maximum une seule fois) “ni point d’arrêt”. Ainsi, Poincaré définit un cycle sphérique comme une courbe qui revient à son point de départ après une longueur finie (voir figure 4a). Il définit ensuite une spirale sphérique comme une courbe “qui coupe un cycle sphérique en un seul point” (Poincaré, 1881, 379), comme illustré dans la figure 4b, où la spirale sphérique est en noire et le cycle sphérique en vert. Poincaré indique également qu’un cycle sphérique sépare la sphère en deux régions, appelées “intérieur” et “extérieur”, et dont on ne peut passer de l’un à l’autre sans devoir couper le cycle (voir figure 4a). Jean Mawhin, dans son article Poincaré’s early use of Analysis situs in nonlinear differential equation: Variations around the theme of Kronecker’s integral (Mawhin, 2000), note que les concepts d’intérieur et d’extérieur sont issus de la topologie, et correspondent à ce qu’on appelle aujourd’hui le théorème de Jordan.

Poincaré explique qu’en prenant deux points d’une caractéristique et en les joignant à l’aide d’un arc de courbe dont les seules intersections sont ces deux points, l’arc de courbe ainsi que l’arc de caractéristique entre les deux points forment un cycle sphérique. Deux cas peuvent alors se présenter :

Premier cas - Les deux branches de courbes formées par la caractéristique prolongée au delà des deux points que l’on a réunis par un arc de courbe quelconque, sont toutes deux intérieures ou toutes deux extérieures au cycle formé par les deux arcs. Dans ce cas, nous dirons que l’arc de courbe sous-tend l’arc de caractéristique. […]
Deuxième cas - Les deux branches de courbes formées par la caractéristique, prolongée au delà des deux points qu’on a réunis par un arc de courbe quelconque, sont, l’une intérieure, l’autre extérieure au cycle formé par les deux arcs. Dans ce cas, nous dirons que l’arc de courbe sur-tend l’arc de caractéristique.
(Poincaré, 1881, 379)

Figure 4: Illustration des différentes définitions sur les cycles

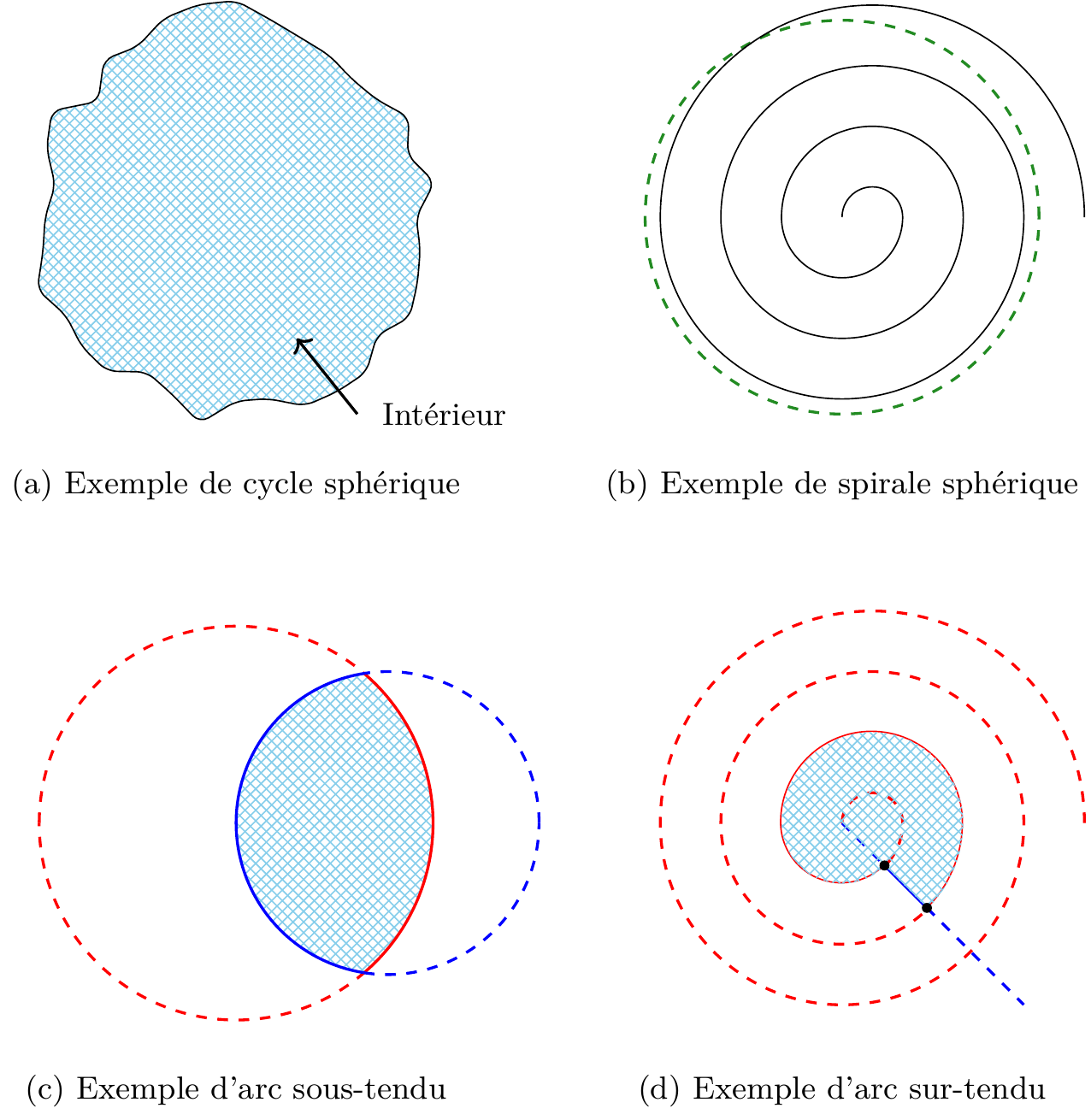
Une illustration de ces deux cas sont les figures (c) et (d) de la figure 4, où les caractéristiques sont représentées en rouge et les arcs de courbe en bleu. Ainsi, dans la figure (c), on voit que la caractéristique prolongée au delà des points d’intersections (en pointillé) est extérieur au cycle formé par la caractéristique et l’arc de courbe (en trait plein). Dans la figure (d), on voit qu’une des branches et à l’intérieur et l’autre à l’extérieur. De ces définitions, Poincaré en tire alors son premier théorème :

Théorème I - Si l’on divise une caractéristique, qui n’offre ni point double, ni point d’arrêt, en deux demi-caractéristiques, si l’une de ces demi-caractéristiques ne coupe aucun cycle algébriques qu’en un nombre fini de points, la caractéristique donne un cycle.
(Poincaré, 1881, 380)

Poincaré définit ensuite un polycycle comme un cycle possédant des points doubles (c’est-à-dire des points d’intersection avec lui-même). La dernière définition de ce chapitre est celle du système topographique, qui est défini comme un ensemble de cycles et de polycycles de telle façon qu’en chaque point de la sphère ne passe qu’un seul cycle ou qu’un seul polycycle, à l’exception de quelques “points singuliers” (Poincaré, 1881), Par exemple, la figure 5(a) représente un système topographique dans le plan, avec un polycycle (en rouge) et quelques cycles (en pointillé bleu). Le point double $A$ peut être vu comme un col, et les points $B$ et $C$ comme des sommets (comme sur la figure 5(b)), les différents cycles et polycycles correspondant alors à des lignes de niveau.

(a) Système topographique dans le plan

(b) Relief imaginaire associé au système topographique

Figure 5: Exemple d’un système topographique et d’un hypothétique terrain correspondant

3.2.2 Chapitre 2 : Étude des caractéristiques dans le voisinage d’un point de la sphère

Dans ce chapitre, Poincaré veut rappeler, avant d’étudier les caractéristiques sur toute la sphère, les résultats déjà développés précédemment sur une région limitée de la sphère. Ces résultats proviennent de Cauchy, de Briot et Bouquet mais également de ses propres travaux antérieures, et il se place alors “dans le cadre d’hypothèses analytiques” (Gilain, 1977, 56), c’est-à-dire qu’il considère ici que $X$ et $Y$ sont des polynômes. Cependant, Gilain indique qu’il y a deux nouveautés chez Poincaré :
1°) $X$ et $Y$, ainsi que les solutions recherchées, sont des fonctions à variables réelles et non complexes.
2°) Il utilise “la signification géométrique des résultats analytiques antérieurs”.
Poincaré fait alors une étude de cas, en considérant un point de coordonnées $x=\alpha,\leavevmode\nobreak\ y=\beta$, les polynômes $X$ et $Y$ peuvent donc être exprimés en fonction de $x-\alpha$ et $y-\beta$ :

$$X=a_{0}+a_{1}(x-\alpha)+a_{2}(y-\beta)+\dots$$

$$Y=b_{0}+b_{1}(x-\alpha)+b_{2}(y-\beta)+\dots$$

Poincaré considère ensuite plusieurs cas :

Premier cas :

$a_{0}$ ou $b_{0}$ non nul, ici il suppose que $a_{0}\neq 0$, l’équation différentielle peut alors s’écrire $\frac{dy}{dx}=\frac{Y}{X}f(x,y)$, où $f$ est une “série ordonnée suivant les puissances croissantes de $x-\alpha$ et $y-\beta$”. Poincaré en conclut d’après un théorème de Cauchy que “$y$ peut s’exprimer par une série ordonnée suivant les puissances croissantes de $x-\alpha$ et se réduisant à $\beta$ pour $x=\alpha$. Donc, par le point $(\alpha,\beta)$ passe une caractéristique et une seule” (Poincaré, 1881, 386)..

Deuxième cas :

$a_{0}=b_{0}=0$, mais $a_{1},\leavevmode\nobreak\ a_{2},\leavevmode\nobreak\ b_{1}$ et $b_{2}$ ne sont pas tous nuls en même temps, Ce point est alors un point singulier ordinaire. Poincaré rappelle ensuite un théorème démontré dans sa thèse :

Si l’équation $(a_{1}-\lambda)(b_{2}-\lambda)-b_{1}a_{2}=0$ a deux racines différentes, $\lambda_{1}$ et $\lambda_{2}$ ; Si le rapport de ces racines est positif ou imaginaire, l’intégrale générale de l’équation $\frac{dx}{X}=\frac{dy}{Y}$ est de la forme $z_{1}^{\lambda_{1}}z_{2}^{-\lambda_{2}}=\text{const.}$, où $z_{1}$ et $z_{2}$ sont des séries ordonnées suivant les puissances croissantes de $x-\alpha,\leavevmode\nobreak\ y-\beta$ et s’annulant pour $x=\alpha,\leavevmode\nobreak\ y=\beta.$
(Poincaré, 1881, 386)

Poincaré distingue alors quatre cas subordonnés, en fonction des valeurs de $\lambda_{1}$ et $\lambda_{2}$ :
1°) Si $\lambda_{1}$ et $\lambda_{2}$ sont réels et de même signe, alors il passe en ce point une infinité de caractéristique : ce point est alors un nœud.
2°) Si $\lambda_{1}$ et $\lambda_{2}$ sont réels et de signe opposé, alors il passe en ce point deux caractéristiques : ce point est un col.
3°) Si $\lambda_{1}$ et $\lambda_{2}$ sont complexes et conjugués avec leur partie réelle non nulle, alors les caractéristiques autour de ce point sont des spirales : ce point est alors un foyer
4°) Si $\lambda_{1}$ et $\lambda_{2}$ sont imaginaires pures opposées, alors les caractéristiques autour de ce point sont des cycles : ce point est alors un centre.
Il reste alors certain cas particuliers : $\lambda_{1}=\lambda_{2}$ et $\lambda_{1}=0$. Pour ce qui du premier, Poincaré indique que pour avoir $\lambda_{1}=\lambda_{2}$, il suffit que $(a_{1}+b_{2})^{2}-b_{1}a_{2}+a_{1}b_{2}=0$, et Briot et Bouquet ont alors déjà indiqué qu’il y avait alors une infinité de caractéristique qui passait par ce point, c’est-à-dire que ce point est un nœud. Ces cinq cas développés par Poincaré correspondent aux point singuliers ($\alpha,\beta$) où les courbes $X=0$ et $Y=0$ s’y coupent une seule fois (ce ne sont pas plusieurs points d’intersection confondus). Poincaré les appelle points singuliers de première espèce, qui peuvent donc être de quatre sortes : nœuds, cols, foyers et centres.
Il reste finalement les cas où $\lambda_{1}=0$, ainsi que les cas où soit $a_{1}=a_{2}=0$, soit $b_{1}=b_{2}=0$. Ces cas se présentent lorsque les courbes $X=0$ et $Y=0$ “se coupent en plusieurs points confondus au point $(\alpha,\beta)$, ces points seront appelés points singuliers de seconde espèce.

Cet intérêt de Poincaré pour l’étude et la classification des points singuliers, à une époque où l’étude analytique des équations différentielles est dominante, n’est cependant pas unique. V. A. Dobrovolsky, dans son article Sur l’histoire de la classification des points singuliers des équations différentielles, indique qu’au cours de années 1875-1890, “les catégories essentielles de points singuliers des fonctions de la variable complexe ont été déterminées et de même le comportement de ces fonctions dans leur voisinage a été caractérisé” (Dobrovolsky, 1972, 5), notamment comme nous l’avons vu précédemment, avec Briot et Bouquet qui se sont intéressés à ces points particuliers.
Dobrovolsky indique par la suite que Poincaré n’est pas le premier à découvrir les différents types de points singuliers de l’équation $\frac{dy}{dx}=\frac{Y(x,y)}{X(x,y)}$, avec $X$ et $Y$ des polynômes réels, mais c’est plutôt le mathématicien russe Zhukovsky en 1876 dans sa thèse de maîtrise intitulé Kinematika jidkogo tela (Cinématique d’un corps liquide) (Zhukovsky, 1876a, b), cette thèse ayant pour objet central “l’étude de la théorie des vitesses et des accélérations de liquides d’un point de vue unitaire” (Dobrovolsky, 1972, 8). Zhukovsky s’intéresse ainsi au mouvement d’une particule de liquide infiniment petite, et obtient alors “les équations différentielles des lignes de courant des points de la particule” :

$$\frac{dx}{e_{1}x-ry}=\frac{dy}{e_{2}y+rx}=\frac{d\xi}{\epsilon_{3}\xi}.$$

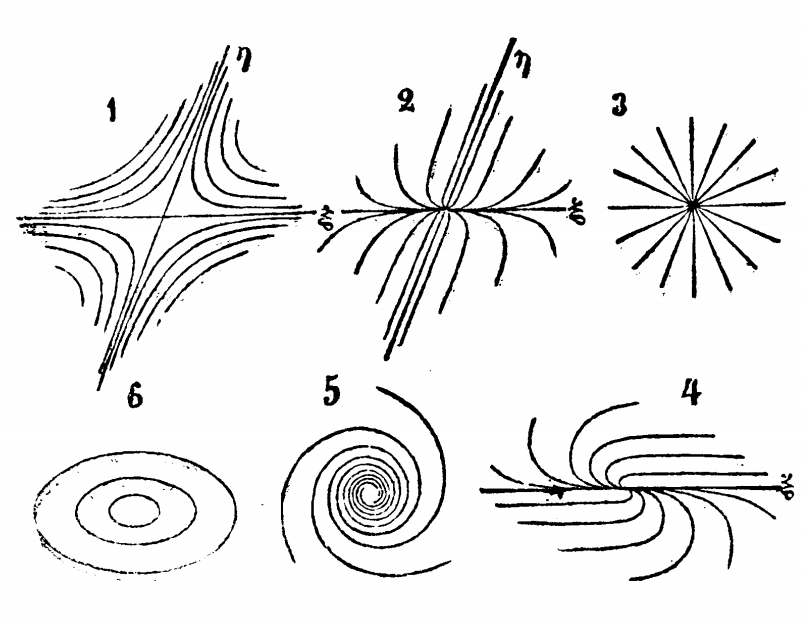
Dans la suite de son étude, il découvre que les lignes de courant ne peuvent pas se toucher ou se croiser, et donc qu’en chaque point d’une ligne de courant il y a une seule valeur déterminée, à l’exception de certains points qu’il appelle alors points “critiques”, qu’il étudie ainsi que les courbes intégrales dans leur voisinage. La figure 6 correspond à cette étude, et l’on peut observer sur les figures 2,3 et 4 des nœuds, sur la figure 1 un col, sur la figure 5 un foyer et sur la figure 6 un centre, cependant cette classification des points singuliers est celle de Poincaré, car Zhukovsky n’a pas nommé les différents types de points qu’il a découvert.

Figure 6: Figure tirée de la thèse de maîtrise de Zhukovsky

Dobrovolsky conclut son article en indiquant que cette découverte en 1876 par Zhukovsky n’enlève rien à l’importance des travaux de Poincaré, “mais dans l’histoire de la science cette question a une importance de principe et le nom de N. Zhukovsky ne doit pas être oublié lors de l’exposé de ce problème” (Dobrovolsky, 1972, 10).

3.2.3 Chapitre 3 : Distribution des points singuliers

Poincaré s’intéresse maintenant à comment sont disposés les points singuliers sur la sphère. Comme l’indique Gilain dans sa thèse, “il ne s’agit plus ici de l’étude locale de tel ou tel point singulier, mais d’obtenir des renseignements sur l’ensemble des points singuliers, leur nombre, leur nature, sur la sphère global” (Gilain, 1977, 58). Poincaré commence directement ce troisième chapitre avec un théorème :

Théorème II - Tout système de caractéristiques admet des points singuliers.
(Poincaré, 1881, 394)

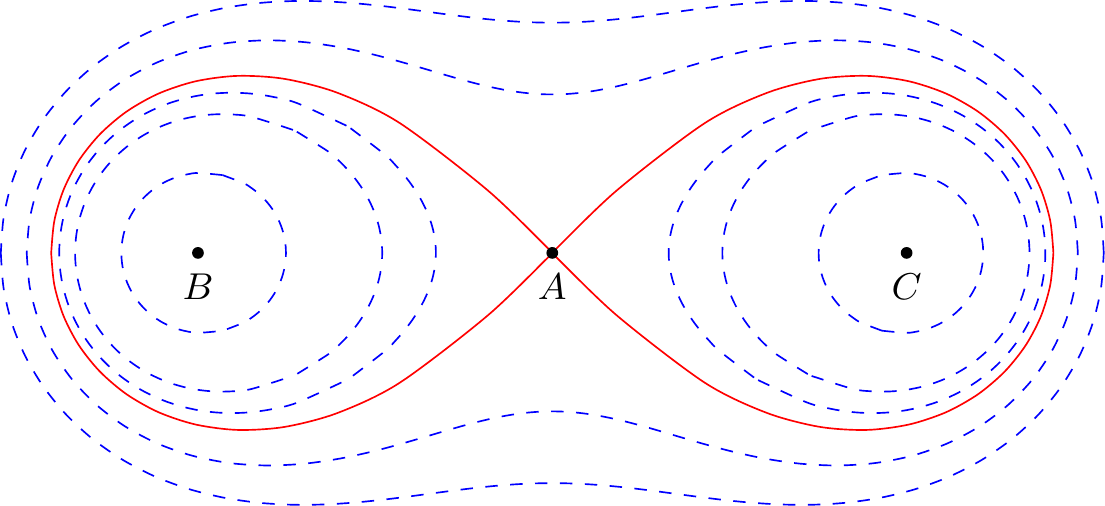
Il précise également qu’il y a toujours un nombre pair de points singuliers par symétrie par rapport au centre de la sphère (voir l’illustration de la projection gnomonique). Poincaré introduit ensuite une “considération nouvelle” qui d’après lui “nous rendra les plus grands services”, cette nouvelle considération est la notion d’indice. Poincaré considère un cycle contenu tout entier dans un hémisphère. Ce cycle, comme nous l’avons vu précédemment, divise la sphère en deux régions, et Poincaré désigne celle contenu tout entière dans l’un des hémisphère comme l’intérieur de ce cycle. Poincaré considère alors un point mobile se déplaçant sur ce cycle, si ce dernier est dans le premier hémisphère, Poincaré dit que le point mobile avance dans le sens positif “s’il a constamment l’intérieur du cycle à sa gauche”, c’est l’inverse si le cycle est dans le second hémisphère. Il suppose alors que ce point mobile se déplace dans le sens positif et considère également “les variations de l’expression $\frac{Y}{X}$”. Il désigne alors par $h$ “le nombre de fois que cette expression saute de $-\infty$ à $+\infty$” et par $k$ “le nombre de fois que cette expression saute de $+\infty$ à $-\infty$”. L’indice $i$ d’un cycle est alors donné par la formule $i=\frac{h-k}{2}$. Poincaré explique alors que l’indice d’un cycle est égale à la somme des indices des cycles qui le compose. Par exemple, sur la figure 7, le cycle $ABCDA$ se décompose en deux cycles : $ABCMA$ et $AMCDA$, et on a donc $\text{ind. }ABCDA=\text{ind. }ABCMA+\text{ind. }AMCDA$.

Figure 7: Reproduction de la figure 2 du mémoire

Poincaré introduit alors son troisième théorème :

Théorème III - Un cycle infiniment petit qui ne contient à son intérieur aucun point singulier a pour indice 0.
(Poincaré, 1881, 401)

En effet, si ce cycle ne contient aucun point singulier, cela signifie que les courbes $X=0$ et $Y=0$ ne se coupent pas dans son intérieur. Ainsi, si il n’est pas coupé par la courbe $X=0$, on a $h=0,\leavevmode\nobreak\ k=0$, et donc $i=\frac{h-k}{2}=0$. Au contraire le cycle est coupé par la courbe $X=0$, alors il n’est pas coupé par la courbe $Y=0$, et donc “$Y$ est toujours du même signe et $X$ passe une fois du positif au négatif, une fois du négatif au positif”, et l’on a alors $h=1,\leavevmode\nobreak\ k=1$ et donc $i=\frac{h-k}{2}=0$. Le résultat est le même si la courbe $X=0$ possède un point multiple à l’intérieur du cycle. Dans la continuité du développement de la notion d’indice, Poincaré s’intéresse aux cycles contenant un point singulier :

Théorème IV - Si un cycle infiniment petit contient à son intérieur un point singulier, son indice est égale à $\pm 1$.
Il est égale à $+1$ si le point singulier est un col ; à $-1$ si le point singulier est un nœud ou un foyer.
(Poincaré, 1881, 401)

Ce théorème est ensuite accompagné de trois corollaires précisant le nombre total de points singuliers :

Corollaire I - Le nombre total des nœuds et des foyers est égal au nombre total des cols plus 2.
Corollaire II - Le nombre total des points singuliers est un multiple de 4 plus 2.
Corollaire III - Si le nombre des points singuliers se réduit à 2, ces points sont des nœuds et des foyers ; ils sont toujours des nœuds s’ils sont sur l’équateur.
(Poincaré, 1881, 405)

Dans le dernier théorème de ce chapitre, Poincaré indique la nature de deux points singuliers consécutifs :

Théorème V - Supposons que deux points consécutifs $\alpha_{k}$ et $\alpha_{k+1}$ soient situés dans le même hémisphère ; je dis que si $\alpha_{k}$ est un nœud ou un foyer, $\alpha_{k+1}$ est un col, ou réciproquement.
(Poincaré, 1881, 405)

Ainsi, l’introduction d’un nouveau concept, celui de l’indice d’un cycle, permet à Poincaré de développer des résultats très utiles dans l’étude des équations différentielles, notamment en liant le nombre de cols, foyers et nœuds d’une équation différentielle. Jean Mawhin, dans Poincaré’s early use of Analysis situs in nonlinear differential equation: Variations around the theme of Kronecker’s integral (Mawhin, 2000), nous indique que ce concept d’indice est lié à celui introduit par Cauchy entre 1831 et 1837, concept qui a été enseigné par Charles Hermite à l’École Polytechnique et à la Sorbonne. Mawhin nous rappelle alors, pour $f$ une fonction rationnelle réelle et un intervalle $[a,b]$, la définition d’un index de Cauchy $\mathcal{I}_{a}^{b}(f)$ sur cet intervalle :

$$\mathcal{I}_{a}^{b}(f)=\#\{t\in[a,b]\leavevmode\nobreak\ :\leavevmode\nobreak\ f(t-)=-\infty,\leavevmode\nobreak\ f(t+)=+\infty\}-\#\{t\in[a,b]\leavevmode\nobreak\ :\leavevmode\nobreak\ f(t-)=+\infty,\leavevmode\nobreak\ f(t+)=-\infty\}.$$

On retrouve en effet chez Poincaré la volonté de compter le nombre de fois où un cycle saute de $+\infty$ à $-\infty$ et de $-\infty$ à $+\infty$. Jean Mawhin insiste également sur l’utilisation de l’indice par Poincaré pour caractériser les points singuliers (cela correspond aux théorème V rappelé précédemment).

3.2.4 Chapitre IV : Théorie des contacts

Poincaré s’intéresse dans ce chapitre aux “formes géométriques que peuvent affecter les caractéristiques sur toute la surface de la sphère” (Poincaré, 1881, 409), étude possible grâce à celle effectué précédemment sur les points singuliers. Poincaré rappelle que l’on peut décomposer un cycle algébrique sans point double en plusieurs cycles, et qu’un cycle algébrique possédant un ou plusieurs points doubles peut être décomposer en plusieurs cycles et polycycles. Il rappelle également “qu’une courbe algébrique $C$ coupe un cycle algébrique quelconque en un nombre fini et pair de points” (Poincaré, 1881, 410). Poincaré explique ensuite comment il compte le nombre de contact entre un cycle et une courbe algébrique $C$ :
- Si la courbe $C$ traverse le cycle (passe de l’intérieur à l’extérieur du cycle ou inversement), ce point d’intersection “comptera pour un seul point d’intersection ou pour un nombre impair de points d’intersection confondus”.
- Si la courbe touche le cycle sans le traverser (elle reste à l’intérieur ou à l’extérieur du cycle dans un voisinage du point de contact), “ce point comptera pour un nombre pair de points d’intersection confondu”.
Poincaré énonce alors le théorème suivant déterminant le nombre de contact entre un cycle algébrique et une caractéristique :

Théorème VI - Le nombre des contacts d’un cycle algébrique qui n’a pas de point anguleux, qui n’a pas de contact d’ordre supérieur avec une caractéristique et qui ne passe par aucun point singulier est toujours fini et pair.
(Poincaré, 1881, 411)

Poincaré accompagne ce théorème de cinq remarques qu’il résume un peu plus loin, ainsi que d’un corollaire :

Résumé - Le nombre des contacts d’un cycle algébrique est toujours pair à la condition :
1°) Que l’on compte un contact du n^ième ordre pour $n$ contacts;
2°) Qu’un point anguleux du cycle donné soit considéré comme un ou comme deux contacts, selon que la caractéristique qui y passe y touche ou y traverse le cycle ;
3°) Qu’un point singulier compte pour $n+1$ contacts si le cycle a, en ce point, un contact du n^ième ordre avec une caractéristique ;
4°) Qu’un foyer qui est un point anguleux du cycle donné soit compté pour un contact ;
5°) Qu’un col ou un nœud qui est un point anguleux du cycle donné soit compté pour un ou pour deux contacts, selon la position des tangentes au cycle au point anguleux.Corollaire - Si deux arcs algébriques ont mêmes extrémités, le nombre de leurs contacts peut être de même parité ou de parité différentes si les deux extrémités ne sont pas deux foyers ; il est toujours de même parité si les deux extrémités sont deux foyers.
(Poincaré, 1881, 415)

Les quatre derniers théorèmes (du théorème VII au théorème X) de la première partie du mémoire continuent de développer cette théorie des contacts, en développant les propriétés des arcs algébriques notamment :

Théorème VII - Si, entre deux points de la sphère, on peut mener un arc quelconque sans contact, on peut aussi mener entre ces deux points un arc algébrique sans contact. […]
Théorème VIII - Si $AB$ est un arc algébrique sans contact, si $AA_{1}$ et $BB_{1}$ sont deux arcs de caractéristiques, on peut mener de $A_{1}$ à $B_{1}$ un arc sans contact. […]
Théorème IX - Si $AB$ et $A_{1}B_{1}$ […] sont deux caractéristiques, si $AA_{1}$ et $BB_{1}$ sont deux arcs algébriques qui ne coupent $AB$ et $A_{1}B_{1}$ en aucun autre point que $A,\leavevmode\nobreak\ B,\leavevmode\nobreak\ A_{1}$ ou $B_{1}$, les nombres des contacts de $AA_{1}$ et de $BB_{1}$ sont de même parité. […]
Théorème X - Si un arc de caractéristique qui ne passe par aucun point singulier est sous-tendu par un arc de courbe, le nombre des contacts de cet arc de courbe est impair.
(Poincaré, 1881, 415-420)

Poincaré indique par la suite que si l’arc de caractéristique passe par un col, il faut modifier le théorème : si il y a de plus un point anguleux, “le nombre des contacts de l’arc sous-tendant est pair”. Au contraire s’il n’y a pas de point anguleux il est impair. Il ajoute également qu’un arc de caractéristique ne passant par aucun point singulier a un nombre de contact pair avec toute les courbes qui le sur-tend.

3.3 La seconde partie du mémoire

Cette partie du mémoire correspond à celle retranscrite dans la deuxième partie de ce travail.

3.3.1 Chapitre V : Théorie des conséquents

Poincaré commence ce chapitre par ce qu’il désigne une “convention fondamentale”. Il considère tout d’abord une demi-caractéristique, et indique que l’on peut la prolonger indéfiniment à moins que l’on rencontre un point singulier :
- Si l’on rencontre un nœud en suivant la demi-caractéristique, on l’arrête à ce nœud.
- Si l’on rencontre un col, alors trois chemins se présente à nous, un “dans le prolongement du chemin suivi jusqu’alors”, ainsi qu’un à gauche et un à droite.
Poincaré décide alors qu’il faudra toujours suivre soit le chemin de gauche, soit celui de droite, mais jamais celui dans le prolongement du chemin d’où l’on vient. Ainsi, au voisinage d’un col, “il y a quatre caractéristiques collées les unes contre les autres, et ayant deux à deux une branche commune” (Poincaré, 1882, 252). Poincaré définit ensuite ce qu’il entend par conséquent :

Définition des conséquents :

Poincaré considère un arc algébrique sans contact dont les coordonnées sont données de la façon suivante :

$$(x,y)=(\varphi(t),\psi(t)),$$

où $\varphi$ et $\psi$ sont des fonction algébriques de $t$ et “n’ont qu’une seule valeur pour chaque valeur de $t$”. Les extrémités de cet arc correspondront aux valeurs $\alpha$ et $\beta$ de $t$. Un tel arc possède une gauche et une droite, de tel façon qu’un point “infiniment voisin” de cet arc se trouvant à gauche (ou à droite) ne puisse passer à droite (ou a gauche) qu’en traversant l’arc ou en s’en éloignant.
Poincaré nomme cet arc algébrique $AB$, et considère un point $M_{0}$ de cet arc, dont partent deux demi-
caractéristiques, une à gauche et une à droite de $AB$, on considère ici celle de gauche. Il y a alors plusieurs cas possible, explicités par Poincaré :
1°) La demi-caractéristique ne rencontre pas l’arc $AB$. En effet elle peut soit être prolongée indéfiniment (sans toutefois rencontrer de nouveau l’arc $AB)$, soit finir par tourner autour d’un foyer, ou soit atteindre un nœud. Dans ces trois cas, on dira alors que “le point $M_{0}$ n’a pas de conséquent”.
2°) La demi-caractéristique rencontre de nouveau l’arc $AB$ en un point que l’on appelle $M_{1}$ avant d’avoir passé un point singulier. Le point $M_{1}$ sera alors le conséquent du point $M_{0}$.
3°) La demi-caractéristique peut également atteindre un col avant de rencontrer de nouveau l’arc $AB$. D’après la convention fondamentale il faut alors tourner à gauche ou à droite, et ces chemins peuvent rencontrer ou non l’arc $AB$. Le point $M_{0}$ peut alors avoir entre 0 et 2 conséquents. La demi-caractéristique peut cependant rencontrer plusieurs cols et donc avoir plus de deux conséquents.
Si, au lien de considérer la demi-caractéristique de gauche on choisissait celle de droite, on pourrait rencontrer l’arc $AB$ en un point que l’on nomme $M^{\prime}$, qui serait alors “l’antécédant du point $M_{0}$”.
Poincaré définit ensuite $t_{0}$ et $t_{1}$ comme les valeurs de $t$ correspondantes à $M_{0}$ et $M_{1}$, et appelle “loi de conséquence” la relation liant $t_{0}$ et $t_{1}$. Il utilise ensuite cette notion de conséquent pour déterminer la forme géométrique de la caractéristique :

Théorème XI - Si $t_{0}=t_{1}$, la caractéristique est un cycle. Si $t_{0}\overset{<}{>}t_{1}$, la caractéristique est une spirale.
Théorème XII - Toute caractéristique qui n’aboutit pas à un nœud est un cycle ou une spirale.
(Poincaré, 1882, 254–255)

Poincaré conclut ce chapitre avec le théorème XIII, les corollaires associés ainsi que le théorème XIV qui portent sur la loi de conséquence, notamment comment caractériser une caractéristique à l’aide de la loi de conséquence associée :

Théorème XIII - Si $M_{0}$ ne correspond pas à une caractéristique passant par un col, s’il a un conséquent $M_{1}$ ; si $t_{1}=\varphi_{1}(t_{0})$ est la loi de conséquence, la fonction $\varphi_{1}$ est holomorphe pour les valeurs de $t_{0}$ voisines de celle qui correspond à $M_{0}$.
Corollaire I - La fonction $t_{1}=\varphi_{1}(t_{0})$, qui exprime la loi de conséquence, ne peut offrir de discontinuité que pour les valeurs de $t_{0}$ qui correspondent à des caractéristiques passant par des cols.
Corollaire II - Si l’on divise l’arc sans contact $AB$ en arc partiels, tels que tous les points de chacun de ces arcs aient un conséquent, ou qu’aucun n’en ait, les extrémités de ces arcs partiels seront des points ayant pour conséquent une extrémité de l’arc sans contact $AB$, ou correspondant à des caractéristiques passant par des cols.
Corollaire III - Si les extrémités de l’arc sans contact correspondent aux valeurs $t=\alpha,\leavevmode\nobreak\ t=\beta$ ; si, pour aucune valeur de $t$ telle que $\alpha<t<\beta$, la caractéristique correspondante ne passe pas par un col; Si, pour toutes les valeurs de $t$, telles que ($\alpha$ et $\beta$ étant des constantes données), on ait $\alpha<\alpha_{1}<t<\beta_{1}<\beta$, la caractéristique correspondante est un cycle. Les caractéristiques qui correspondent à une valeur quelconque de $t$ comprise entre $\alpha$ et $\beta$ sont toutes des cycles
Théorème XIV - La valeur de $\frac{dt_{0}}{dt_{0}}$ est toujours positive
(Poincaré, 1882, 255)

3.3.2 Chapitre VI : Théorie des cycles limites

Dans ce chapitre, Poincaré s’intéresse ici à une catégorie de caractéristique, celle des “spirales que l’on peut suivre indéfiniment dans les deux sens sans aboutir à un nœud ou sans tourner autour d’un foyer, et sans revenir au point de départ” (Poincaré, 1882, 262), plus précisément aux demi-spirales, afin d’introduire un concept important : les cycles limites.

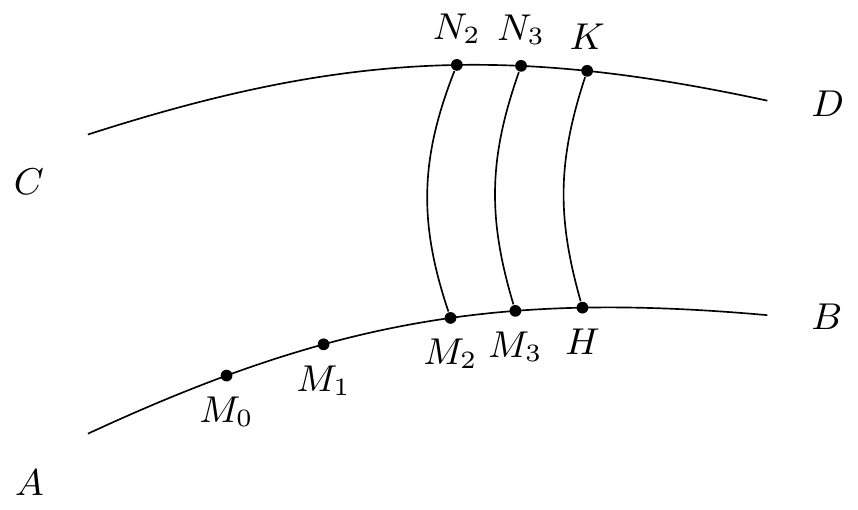
Il considère tout d’abord un arc algébrique $AB$ sans contact, ainsi qu’un point $M_{0}$ d’où part une demi-spirale. D’après le théorème I, cette caractéristique va rencontrer cet arc algébrique en une infinité de point. Il nomme alors $M_{1}$ le conséquent de $M_{0}$, $M_{2}$ le conséquent de $M_{1}$, etc., avec $M_{1}$ à droite de $M_{0}$, $M_{2}$ à droite de $M_{1}$, etc. D’une façon plus générale, $M_{n+1}$ sera le conséquent de $M_{n}$ et sera à droite de $M_{n}$ (voir figure 8). D’après Poincaré, pour tout $n$, $M_{n}$ sera toujours sur l’arc $AB$, ce qui signifie que $M_{n}$ tend vers une limite qu’il appelle $H$. Plus $n$ est grand, plus le conséquent de $M_{n}$ sera proche de lui, on en déduit que $H$ est son propre conséquent, ainsi la caractéristique qui passe par $H$ est donc un cycle, qu’il appelle “cycle limite” de cette demi-caractéristique.
Poincaré considère alors un arc de ce cycle dont l’une des extrémités est le point $H$, qu’il nomme $HK$, ainsi qu’un arc algébrique $CD$ passant par $K$. Pour chaque point $M_{n}$, l’arc de caractéristique issue de ce point rencontrera $CD$ au point $N_{n}$. Comme pour les points $M_{n}$, $N_{n+1}$ sera à droite de $N_{n}$, et cette suite de point tend alors vers $K$. Poincaré conclut son raisonnement par “toute demi-caractéristique de la seconde catégorie a un cycle limite”.

Figure 8: Reproduction de la figure 16 du mémoire

Poincaré introduit alors le théorème XV :

Théorème XV - A l’intérieur et à l’extérieur d’un cycle limite quelconque, il y a toujours au moins un foyer ou un nœud.
(Poincaré, 1882, 264)

Ce théorème permet alors de prouver le théorème XVI, qui stipule qu’un “cycle algébrique qui passe par tous les nœuds et par tous les foyers rencontre tous les cycles limites” (Poincaré, 1882, 269); En effet, d’après le théorème précèdent, en prenant un cycle limite $C$, il y a toujours au moins un nœud ou un foyer à l’intérieur et à l’extérieur de ce cycle, un cycle passant par tous les nœuds et par tous les foyers est donc obligé de couper ce cycle limite. Le dernier théorème sur les cycles limites est le théorème XVII :

Théorème XVII - Les cycles limites sont en nombre fini, pourvu qu’aucun ne passe par un col.
(Poincaré, 1882, 269)

Poincaré développe ensuite ce qu’il appelle la “théorie des anneaux limites”. Il détermine qu’il existe une région annulaire autour d’un cycle limite, délimitée par deux cycles sans contact qu’il nomme “cycles frontières”. Cette région est parcourue de “cycles sans contact qui ne se coupent en aucun point” (Poincaré, 1882, 271). Il nomme alors ces régions annulaires “anneaux limites” qui seront en nombre fini.
Poincaré indique par la suite que les cycles frontières “divisent la sphère en deux catégories de régions” :
1°) Les anneaux limites, définis précédemment
2°) Les régions interannulaires.
D’après Poincaré, si l’on parcours une caractéristique en partant d’une région interannulaire, on arrivera forcément dans un anneau limite après avoir traversé un cycle frontière. La raison est que les régions interannulaires “ne contiennent ni nœud, ni foyer, ni aucun point des cycles limites, et sont, comme les anneaux limites, parcourues par des cycles sans contact.
Poincaré conclut ce chapitre avec le théorème XVIII :

Théorème XVIII - Il existe toujours un système topographique formé de cycles sans contact, de polycycles sans contact et de cycles limites. Ce système topographique sillonne toute la surface de la sphère. Les fonds et ses sommets sont les nœuds et les foyers de l’équation donnée. Les cols sont les cols de l’équation données.
(Poincaré, 1882, 274)

Ainsi, d’après Poincaré, connaître ce système topographique permet de savoir quelle forme qu’auront les courbes définies par l’équation différentielles.

Ce chapitre du mémoire introduit donc un des nouveaux concepts clés de Poincaré, celui des cycles limites, une nouvelle catégorie de courbes fermés. Ainsi, dans l’Analyse des Travaux Scientifiques de Henri Poincaré, dont il est l’auteur, il définit ces cycles limites comme des “courbes fermées qui satisfont à notre équation différentielle et dont les autres courbes définies par la même équation différentielle se rapprochent asymptotiquement sans jamais les atteindre.” (Poincaré, 1921, 58). Pour illustrer cette définition, Poincaré considère un point mobile suivant une trajectoire (ou caractéristique) définie par une équation différentielle. Si cette trajectoire correspond à un cycle limite, alors elle prend la forme d’une courbe fermée, qui attire les autres trajectoires, autant celle qui se trouve en son intérieur qu’à l’extérieur. Jean Mawhin dans (Mawhin, 2000), indique que d’un point de vue topologique, la propriété essentielle des cycles limites est le théorème XV : “A l’intérieur et à l’extérieur d’un cycle limite quelconque, il y a toujours au moins un foyer ou un nœud” (Poincaré, 1882, 269), qui est comme l’explique Mawhin la conséquence du calcul de l’indice d’un cycle limite, qui nous donne $-1$.
Jean-Marc Ginoux dans Henri Poincaré et l’émergence du concept de cycle limite (Ginoux, 2012), indique que du point de vue mathématique, Poincaré met en avant un nouvelle catégorie de “courbes définies par une équation différentielles”. Du point de vue de la physique, cela nous indique que “quelles que soient les conditions initiales choisies, la trajectoire s’approche asymptotiquement de la courbe fermée sans jamais l’atteindre” (Ginoux, 2012, 2), mais d’après Ginoux, cette explication ne nous renseigne pas sur sa signification, et il faudra d’après lui attendre 1908 pour que Poincaré donne son interprétation. En effet les cycles limites, d’un point de vue physique, correspondent aux solutions périodiques d’une équation différentielle représentant les oscillations d’un système auto-entretenues, c’est-à-dire d’un “système dont les oscillations sont entretenues par le système lui-même” (Ginoux, 2012, 3).
Pendant longtemps l’historiographie considérait cependant que Poincaré “n’avais jamais mis en application le concept de cycle limite” (Ginoux, 2012, 6), et que l’on devait son interprétation physique à Aleksandr’ Andronov (1901-1952), un mathématicien russe, qui fit la correspondance entre cycle limite et solution périodique d’un système auto-entretenus en 1929. Cependant, la découverte de conférences de Poincaré en mai-juin 1908 à l’école Supérieure des Postes et Télégraphes a révélé que Poincaré avait bien fait cette correspondance, qui plus est un peu plus de 20 ans avant Andronov.

3.3.3 Chapitre XVII : Exemples de discussions complètes

Dans ce chapitre, Poincaré donne plusieurs exemples d’étude complète d’équations différentielles mettant en application toutes les notions introduites précédemment. Le quatrième de ces exemples a été plus développé par Gilain dans sa thèse (Gilain, 1977), il me semble donc intéressant pour illustrer ce chapitre.

On cherche ici à étudier le comportement des caractéristiques de l’équation différentielle $\frac{dx}{X}=\frac{dy}{Y}$ suivante :

$$\frac{dx}{x(x^{2}+y^{2}-1)(x^{2}+y^{2}-9)-y(x^{2}+y^{2}-2x-8)}=\frac{dy}{y(x^{2}+y^{2}-1)(x^{2}+y^{2}-9)+x(x^{2}+y^{2}-2x-8)}$$

La première étape est de trouver les points singuliers, il y en a trois : le point $O=(0,0)$ ainsi que les points d’intersection $A$ et $B$ des cercles $x^{2}+y^{2}-9=0$ et $x^{2}+y^{2}-2x-8=0$. Il faut maintenant déterminer la nature de ces points singuliers.

Commençons par le point $O$ : $X$ et $Y$ peuvent être réécris de la manière suivante :

$$X =9x+8y+X_{2},$$

$$Y =-8x+9y+Y_{2},$$

avec $X_{2}$ et $Y_{2}$ les termes du degré le plus élevé de $X$ et $Y$. On a alors $a_{0}=b_{0}=0$, $a_{1}=b_{2}=9$ et $b_{1}=-a_{2}=-8$, ce qui nous donne l’équation caractéristique suivante :

$$(a_{1}-\lambda)(b_{2}-\lambda)-b_{1}a_{2}=0 \Leftrightarrow(9-\lambda)(9-\lambda)+64=0$$

$$\Leftrightarrow(9-\lambda)^{2}+64=0$$

Les solutions de l’équation sont $\frac{9\pm i\sqrt{499}}{2}$, les deux racines sont donc imaginaires conjugués avec une partie réelle non nulle : le point $O$ est donc un foyer.

Pour les points $A$ et $B$, on commence par les calculer, c’est-à-dire à résoudre l’équation $x^{2}+y^{2}-9=x^{2}+y^{2}-2x-8$ :

$$x^{2}+y^{2}-9 =x^{2}+y^{2}-2x-8$$

$$\Leftrightarrow-9 =-2x-8$$

$$\Leftrightarrow x =\frac{1}{2}\Rightarrow y=\pm\frac{\sqrt{35}}{2}.$$

Soit $A=(\frac{1}{2},\frac{\sqrt{35}}{2})$ et $B=(\frac{1}{2},\frac{-\sqrt{35}}{2})$. Gilain dans sa thèse nous donne la réécriture de $X$ et $Y$ pour le point $A$ :

$$X =a_{1}(x-\frac{1}{2})+a_{2}(y-\frac{\sqrt{35}}{2})+X_{2},$$

$$Y =b_{1}(x-\frac{1}{2})+b_{2}(y-\frac{\sqrt{35}}{2})+Y_{2},$$

avec $a_{1}=4+\frac{\sqrt{35}}{2},\leavevmode\nobreak\ a_{2}=\frac{\sqrt{35}}{4}-\frac{35}{2},\leavevmode\nobreak\ b_{1}=\frac{\sqrt{35}}{4}-\frac{1}{2},\leavevmode\nobreak\ b_{2}=140+\frac{\sqrt{35}}{2}$. L’équation caractéristique associée a alors pour racine deux nombres réelles positifs, $A$ est un nœud. Avec le même raisonnement, on obtient que $B$ est un col.

Sur la sphère, comme chaque point est projeté deux fois (une fois dans le premier hémisphère et une fois dans le second, voir figure 3), on a deux foyers correspondant au point $O$, deux nœuds correspondant au point $A$ et deux cols correspondant au point $B$. Ainsi, on a bien $N+F=C+2$.

On s’intéresse ensuite aux cycles limites et aux cycles sans contact. Gilain nous indique que l’équateur, qui est une caractéristique, ne contient aucun point singulier, est un cycle limite. Il considère ensuite un système composé des cercles de centre $O$, qui peuvent s’écrire $F(x,y)=\text{const.}$. On cherche alors les contacts entre ces cycles et les caractéristiques. Ces contacts sont données par le système suivant :

$$\left\{\begin{array}[]{ll}F(x,y)=x^{2}+y^{2}=\text{const.},\\ X\frac{\partial F}{\partial x}+Y\frac{\partial F}{\partial y}=(x^{2}+y^{2})(x^{2}+y^{2}-1)(x^{2}+y^{2}-9)=0.\end{array}\right.$$

On voit alors que l’ensemble des cercles d’origine $O$ sont sans contact, à l’exception des cercles $x^{2}+y^{2}=1$ et $x^{2}+y^{2}-9=0$ qui sont des caractéristiques. Le premier, qui ne passe par aucun point singulier, est un cycle limite. Le second passe par les points $A$ et $B$. Poincaré indique qu’il y a trois catégories de caractéristiques :
1°) Celles qui tournent autour du foyer $O$, elles ont pour cycle limite le cercle centré sur l’origine de rayon 1.
2°) Celles qui “aboutissent au nœud $A$” et qui ont pour cycle limite le cercle de rayon 1.
3°) Celles qui aboutissent également au nœud $A$ mais qui ont pour cycle limite l’équateur.
Il y a également cinq “caractéristiques exceptionnelles” :

1°) L’équateur ;
2°) Le cercle $x^{2}+y^{2}=1$ ;
3°) Le cercle $x^{2}+y^{2}=9$ ;
4°) Une caractéristique partant du col $B$ et ayant pour cycle limite l’équateur ;
5°) Une caractéristique partant du col $B$ et ayant pour cycle limite $x^{2}+y^{2}=1$ .

Figure 9: Reproduction de la figure 27 du manuscrit

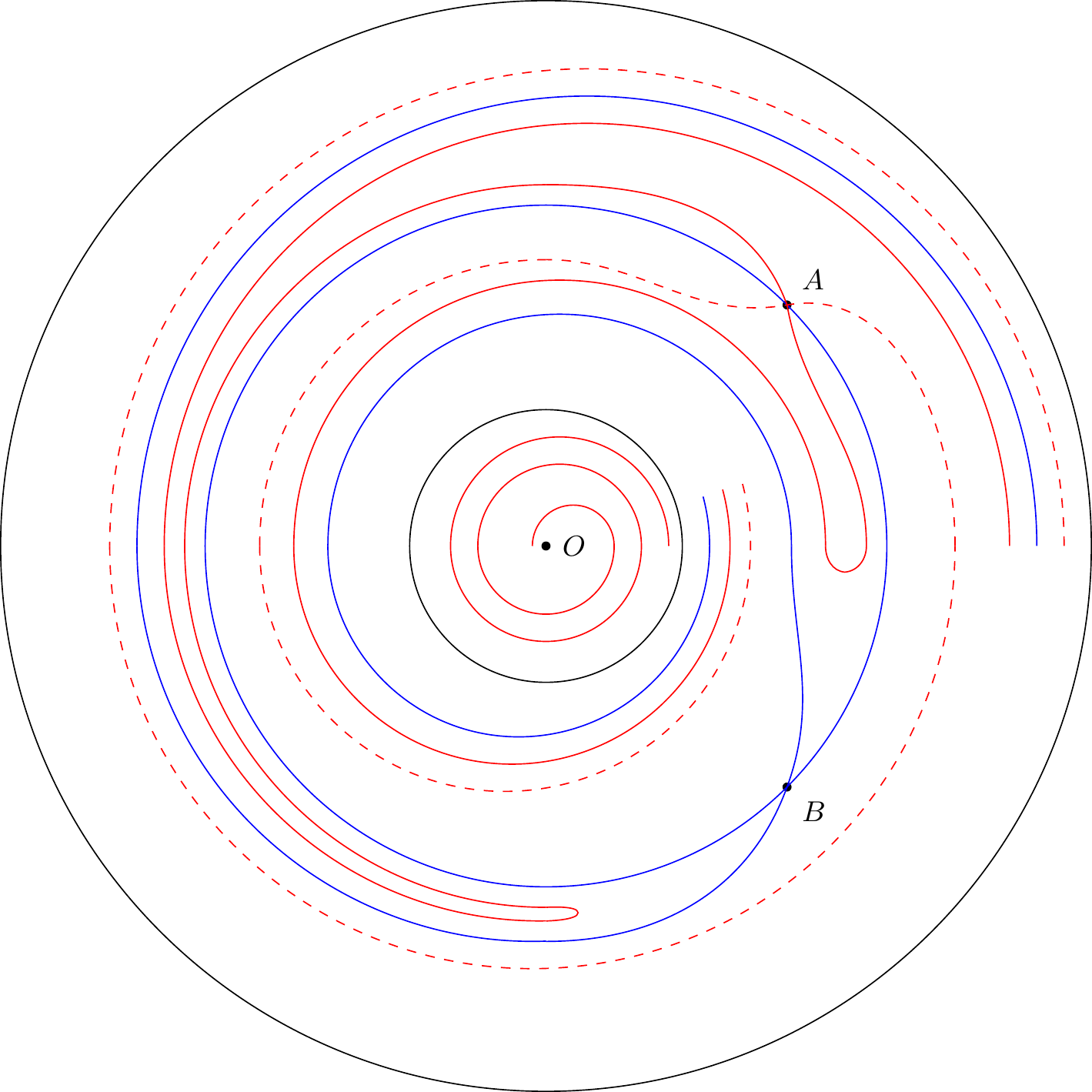
Tout ceci est résumé sur la figure 9, avec les cycles limites en noir, les caractéristiques ordinaires en rouge et pointillé rouge, et les caractéristiques exceptionnelles en bleu.

3.3.4 Chapitre VIII : Recherche des cycles sans contact

Poincaré explique que trouver les cycles limites n’est pas si simple quand ces derniers ne sont pas algébriques. En effet dans les exemples du chapitre précédent, les équations différentielles étudiées sont conçus pour trouver facilement les cycles limites associés qui sont alors algébriques, ce qui permet une discussion “complète”. Malheureusement quand ils ne le sont pas, il est impossible de pouvoir mener l’analyse à son terme. Néanmoins, d’après lui on pourra toujours diviser la sphère en deux types de régions (si le nombre de cycles limites est finis) :
1°) Des régions dans lesquelles il n’y a aucun cycle limite, qu’il appelle régions “acycliques”.
2°) Des régions contenant en entier un cycle limite et un seul, qu’il appelle régions “monocycliques”
Deux autres types de régions sont également introduites par Poincaré : les régions dites “cycliques”, qui “contiennent certainement un cycle limite tout entier, et sont peut-être traversées par un ou plusieurs cycles limites”, et les régions dites “douteuses”, où il y a “peut-être un cycle limite, peut-être plusieurs, et qui peut-être ne sont traversées par aucun cycle limite” (Poincaré, 1882, 284).
Poincaré, dans la suite de ce chapitre, développe une méthode afin de déterminer ces différentes régions, et propose dans dernier chapitre de cette partie (le chapitre IX : Exemples de discussions incomplètes) une application de cette méthode à différent exemples. Je choisis dans ce résumé de ne pas rentrer plus dans les détails de cette méthode, qui est assez calculatoire.

3.4 Conclusion sur les deux premières parties du mémoire

La première partie du mémoire a différents objectifs, le premier étant l’introduction de définitions, de concepts afin d’établir les bases solides du développement d’une nouvelle théorie des équations différentielles portant essentiellement sur leur analyse qualitative. On peut notamment noter qu’une partie de ses définitions viennent de la topologie, comme les notions d’intérieur, d’extérieur et d’indice, mais peuvent également venir de domaine extérieur aux mathématiques, comme les différentes catégories de points singuliers (noeud, foyer, col et centre) qui viennent pour la plupart de la comparaison entre équation différentielle et topographie d’un terrain. Le reste de la première partie est consacrée majoritairement à l’étude des points singuliers, que ce soit leur catégorisation ou leur distribution sur la sphère.
La deuxième partie du mémoire a pour élément principal l’introduction d’un nouveau concept, celui des cycles limites, qui permet de déterminer d’une meilleure façon la forme géométrique des caractéristiques. On retrouve également des exemples dans lesquels Poincaré utilise toutes les définitions, méthodes et concepts introduits dans les deux première parties, mais cette analyse, comme nous le précise Poincaré, est très souvent limité, par exemple dès lors que les cycles limites ne sont plus algébriques.

Notes

• 1 Birkhoff (1934, 1). Version originale : “The usual existence theorems for an ordinary differential system of the first order such as $\frac{dx_{1}}{X_{1}(x_{1},\dots,x_{n}}=\dots=\frac{dx_{n}}{X_{n}(x_{1},\dots,x_{n}}=\frac{dt}{1}$ failed to apply in the neighborhood of the singular points”.
• 2 Birkhoff (1934, 1). Version originale : “$\psi$ is an ordinary convergent power series in $x_{1},\dots,x_{n}$ without constant terms, provided that the singular point in question is taken at the origin of coordinates”.
• 3 Version originale : “the main task was to find the properties of the solution to a differential esuation at all points of the plane, in particular, whether the function is discontinuous or many-valued”.
• 4 Version originale : “the singular points of the solutions mus lie amongst the singular points of the coefficients, and so, in particular, they are fixed”.
• 5 Version originale : “where $P$ et $Q$ are rational functions of a complex variable $z$”.
• 6 Version originale : “of the fact that the order between the two (qualitative and quantitative) parts of the study, sucha as was usual to geometers in elementary questions, is to be reversed when taking higher subjects”.
• 7 Version originale : “beautiful theory of analytic functions”.
• 8 Version originale : “the shortest way between two truths in the real domain very often goes through the complex one”. Cette citation viendrait en fait de Paul Painlevé dans Analyse des travaux scientifiques, publié en 1900.
• 9 On peut également l’écrire sous la forme $N+F=C+2$, avec $N$ le nombre de nœuds, $F$ le nombre de foyer et $C$ le nombre de cols
• 10 Par “seconde catégorie”, il entend les demi-spirales.

Time-stamp: " 2.08.2024 18:15"