footnotebackref\IfPackageLoadedTFbigfoot\IfPackageLoadedTFfontspec\IfPackageLoadedTFcaption\IfPackageLoadedTFcaption-light
Mémoire sur les courbes définies par une équation différentielle
Transcription et annotation par Thomas Marcou du manuscrit de l’article de Poincaré publié dans le Journal des mathématiques pures et appliquées (Poincaré, 1882), réalisée dans le cadre du Master Épistémologie et histoire des sciences, UFR Sciences et techniques, Université de Nantes, en août 2021. Revue et étendue légèrement pour publication éléctronique sur Henri Poincaré Papers par S.A. Walter. Pour une synthèse des travaux d’historiens à ce propos, voir le mémoire de Master 1 de Thomas Marcou.
Chapitre V
Théorie des conséquents
Convention fondamentale :
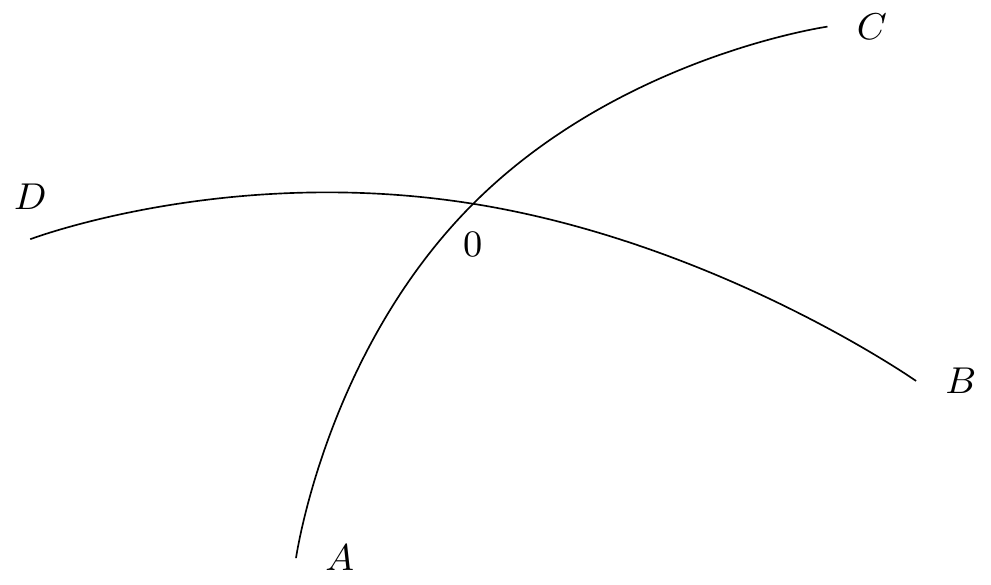
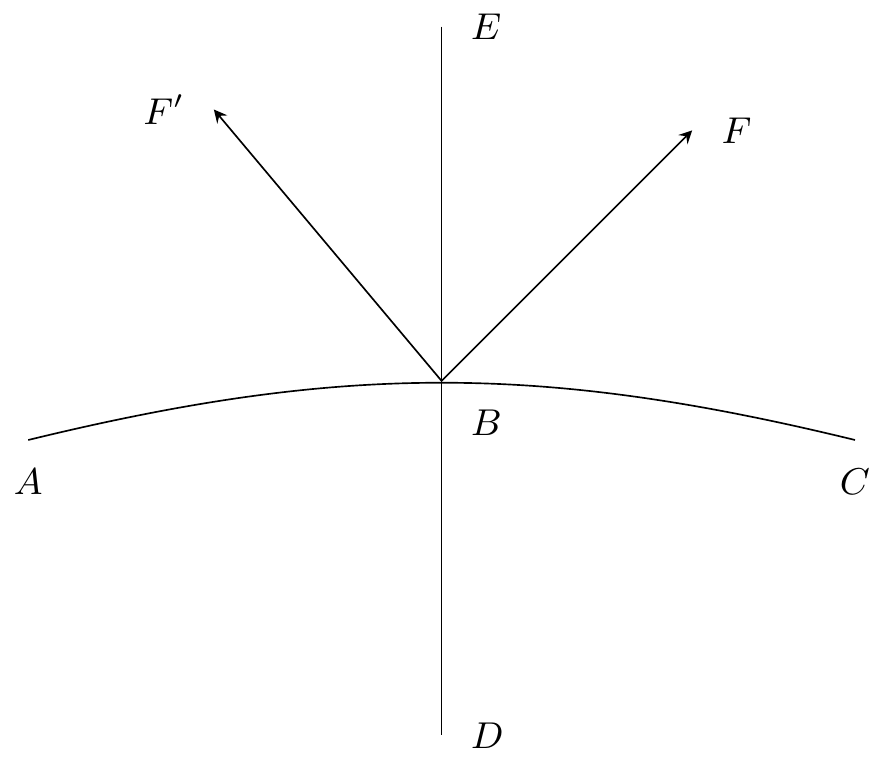
11endnote: 1 Le manuscrit porte une note marginale de main inconnue: “16 Belouze”.Considérons une demi-caractéristique quelconque; nous la prolongerons indéfiniment si on peut le faire sans rencontrer un point singulier; si au contraire, en suivant la demi-caractéristique nous arrivons à un noeud, nous l’arrêterons à un noeud; si nous arrivons à un col, trois chemins s’ouvriront devant nous quand nous voudrons continuer à suivre la caractéristique, premier dans le prolongement du chemin suivi jusqu’alors, les deux autres à droite et à gauche; nous conviendrons de suivre l’un des chemins de droite ou de gauche22endnote: 2 Variante : “nous conviendrons, pour finir les idées, de suivre…”., sans jamais prendre celui qui est directement devant nous. Par exemple, nous considérerons33endnote: 3 Variante : “Par exemple, un point nous considérerons…” ou44endnote: 4 Variante : “ et ou ”. (figure 6)55endnote: 5 Variante : “(figure 2 6)”., et non pas OC66endnote: 6 Variante : “comme et non pas …”. comme le prolongement de . De cette façon on peut dire que dans le voisinage d’un col, il y a quatre caractéristiques collées l’une contre l’autre, et ayant deux à deux une branche commune, ce sont les caractéristiques , , , .
Définition des conséquents :
Soit :
un arc algébrique sans contact; et sont des fonctions algébriques continues77endnote: 7 “continues” a été enlevé dans la version imprimée. de et n’ont qu’une seule valeur pour chaque valeur de . Les extrémités de l’arc correspondront aux valeurs de :
Un pareil arc sans contact aura deux côtés que nous appellerons sa droite et sa gauche; un point infiniment voisin de l’arc pourra en effet être à droite ou à gauche de cet arc. Par exemple, le point sera à gauche de l’arc (figure 7)88endnote: 8 Variante : “(figure 3 7)”., le point à droite de l’arc , parce qu’on ne peut passer de l’un à l’autre sans traverser l’arc , ou sans s’éloigner99endnote: 9 Variante : “…sans s’en éloigner …”. de cet arc à distance finie, ou sans passer dans un cercle de rayon infiniment petit tracé avec ou comme centre.
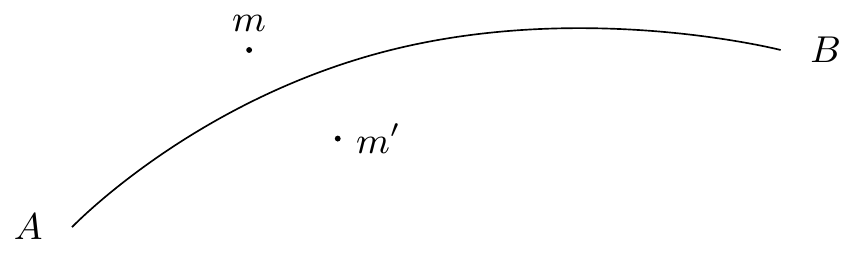
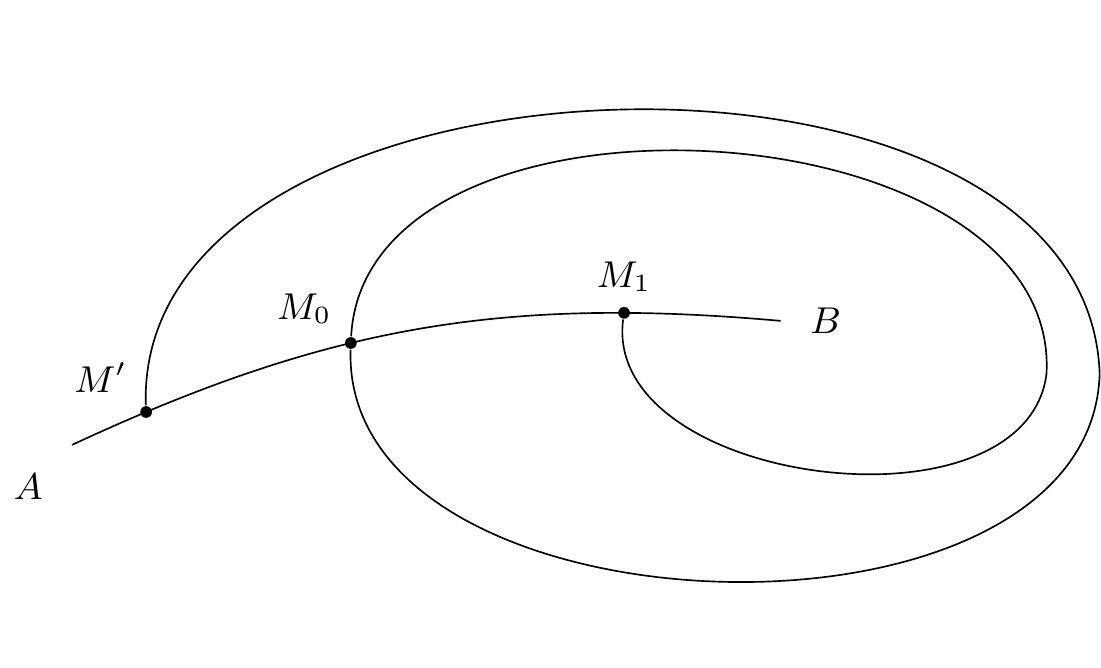
Ceci posé, considérons un point quelconque de l’arc (figure 8)1010endnote:
10
Variante : “(figure 4 8)”.; de ce point partent deux demi caractéristiques, l’une vers la gauche, l’autre vers la droite de l’arc ; considérons celle de gauche.
Il pourra se présenter plusieurs cas :
1°) Cette demi1111endnote:
11
“demi” a été rajouté entre “Cette” et “caractéristique”. caractéristique peut se prolonger indéfiniment sans qu’on rencontre de nouveau l’arc .
2°) Cette demi-caractéristique finit en tournant autour d’un foyer, avant d’avoir rencontré de nouveau l’arc .
3°) Elle aboutit à un noeud où nous devons l’arrêter d’après la convention fondamentale, et cela avant d’avoir rencontré de nouveau l’arc .
Dans ces trois cas, nous dirons que le point n’a pas de conséquent.
4°) La demi caractéristique vient rencontrer l’arc en avant d’avoir passé par un point singulier. Nous dirons alors que le point est le conséquent du point .
5°) La demi caractéristique aboutit à un col avant d’être arrivée à rencontrer de nouveau l’arc . Dans ce cas, et d’après la convention fondamentale, il faut tourner soit à droite, soit à gauche, et chacun de ces deux chemins peut nous conduire ou ne pas nous conduire à rencontrer de nouveau l’arc . Le point peut alors avoir , ou conséquents.
Il peut enfin arriver que la demi caractéristique rencontre deux cols ou plus encore et dans ce cas, le point pourrait avoir plus de 2 conséquents. Si en partant du point 1212endnote:
12
“en partant du point ” a été rajouté entre “Si” et ”au lieu de considérer”. au lieu de considérer la demi caractéristique de gauche, on avait envisagé celle de droite, on aurait pu arriver1313endnote:
13
Variante : “…celle de droite, et qu’on fût arrivé on aurait …”. à un point situé sur l’arc .
Ce point s’appellera l’antécédent du point . Dans ces conditions le point sera lui-même l’antécédent de son conséquent .
Si et sont les valeurs de qui correspondent
à et à , la loi de conséquence sera la relation qui lie à
Théorème XI :
Si , la caractéristique est un cycle.
Si , la caractéristique est une spirale.
En effet la première partie de l’énoncé est une véritable tautologie. La seconde se démontre aisément de la manière suivante :
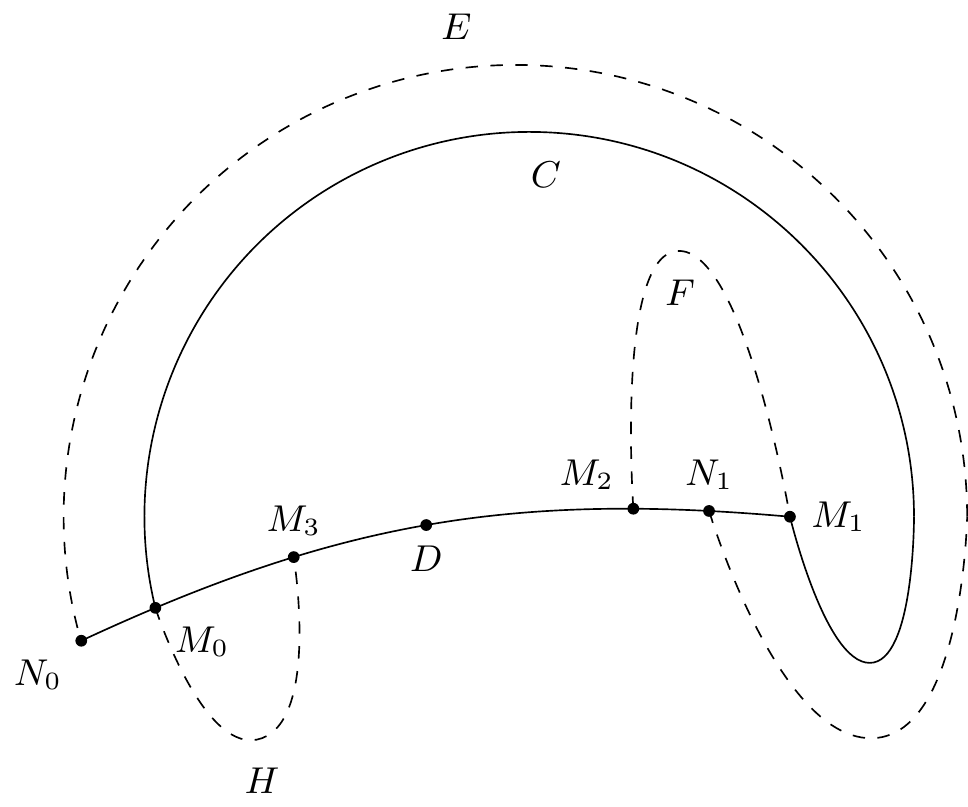
Remarquons d’abord que l’arc (figure 9)1414endnote:
14
Variante : “(figure 5 9)”. sur-tend l’arc de la caractéristique; car il est sans sans contact.
De plus cet arc ne peut rencontrer la caractéristique en aucun autre point que et . Car des arcs tels que , seraient sous-tendus1515endnote:
15
Note présente dans la marge : “Note pour l’imprimeur : Sur l’arc les points se succèdent dans l’ordre suivant : ”. par les arcs , ce qui est impossible puisque ces arcs sont supposés sans contact.
Ceci posé, par le point infiniment voisin de et à gauche de ce dernier, on pourra mener un arc de caractéristique qui viendra rencontrer l’arc en un point infiniment voisin de et à gauche de ce dernier; car il ne pourrait passer à droite sans couper la caractéristique , ce qui est impossible.
Le cycle1616endnote:
16
Variante : “L’arc Le cycle …”. ne rencontre donc la caractéristique qu’en un seul point qui
est . Donc cette caractéristique est une spirale.
C.Q.F.D.
Théorème XII :
Toute caractéristique, qui n’aboutit pas à un noeud, est un cycle ou une spirale.
En effet si cette caractéristique ne rencontre aucun cycle algébrique en une infinité de points, elle est un cycle, en vertu du théorème I.
Si au contraire elle rencontre un cycle algébrique en une infinité de points, comme ce cycle se compose d’un nombre fini d’arcs sans contact, elle rencontrera l’un de ces arcs sans contact en plus d’un point, c’est à dire que l’un des points d’intersections aura un conséquent.
S’il se confond1717endnote:
17
Variante : “…S’il rencontre se confond …”. avec son conséquent, la caractéristique est un cycle, s’il ne se confond pas avec son conséquent, la caractéristique est une spirale, en vertu du théorème XI.
Le théorème est donc démontré.
Théorème XIII :
Si ne correspond pas à une caractéristique passant par un col, et s’il a un conséquent ,1818endnote: 18 La virgule a été remplacé par un point virgule. si 1919endnote: 19 Variante : “…s’il a un conséquent , si et sont les valeurs de qui correspondent à et à si …”. est la loi de conséquence, la fonction 2020endnote: 20 a été corrigé par dans la version imprimée. est holomorphe pour les valeurs de voisines de celle qui correspond à .
En effet2121endnote: 21 Variante : “Soit En effet …”. nous avons supposé au début2222endnote: 22 Variante : “En effet nous supposons avons supposé que …”. que si :
sont les équations de l’arc sans contact, et sont des fonctions holomorphes de dans le voisinage de la valeurs de qui correspond à et aussi de celle qui correspond à .
Supposons que l’on cherche une intégrale de l’équation aux différences partielles
qui soit assujettie à se réduire identiquement à quand on y fait
Cette intégrale représente une surface qui passe2323endnote: 23 Variante : “…une surface qui coupe le cylindre qui a pour base le passe par …”. par la courbe gauche :
Dans le voisinage du point , cette intégrale est holomorphe en et en ; car l’arc
ne touche pas une caractéristique.
Elle sera de même holomorphe en et en tout le long de la caractéristique qui passe par le point à moins que cette caractéristique ne passe par un point singulier. Or, nous avons supposé que cette caractéristique allait passer par le point sans avoir rencontré auncun point singulier. Dans le voisinage du point , est donc fonction holomorphe de et de ; et si on y
fait :
devient fonction holomorphe de dans le voisinage de la valeur de qui correspond à .
Or n’est autre chose que . Donc est fonction holomorphe de . On démontrerait identiquement de la même manière que est fonction holomorphe de dans le voisinage de qui correspond à .
Corollaire I :
La fonction qui exprime la loi de conséquence ne peut offrir de discontinuité que pour les valeurs de qui correspondent à des caractéristiques2424endnote: 24 Variante : “…correspondent à des cols caractéristiques …”. passant par des cols.
Corollaire II :
Si l’on divise l’arc sans contact en arcs partiels, tels que tous les points de chacun de ces arcs aient un conséquent, ou qu’aucun n’en ait, les extrémités de ces arcs partiels seront des points ayant pour conséquent une extrémité de l’arc sans contact , ou correspondant à des caractéristiques passant par des cols.
Corollaire III :
Si les extrémités de l’arc sans contact2525endnote: 25 Variante : “Si l’on divise l’arc sans contact en a Si les extrémités de l’arc sans contact …”. correspondent aux valeurs :
Si pour aucune valeur de telle que
la caractéristique correspondante ne passe pas par un col.
Si pour toutes les valeurs de telles que ( et
étant des constantes données) on ait :
la caractéristique correspondante est un cycle.
Les caractéristiques qui correspondent à une valeur quelconque2626endnote:
26
Variante : “…à une valeur donnée quelconque de …”. de comprise entre et sont toutes des cycles.
Théorème XIV :
La valeur de est toujours positive.
En effet soit l’arc sans contact (figure 10),2727endnote: 27 Variante : “(figure 6 10)”. soit , une caractéristique, soit un point infiniment voisin de et situé à droite de ce point. Soit la caractéristique qui passe par ce point. Le point est infiniment voisin de ; je dis qu’il est à droite de ce point. Car2828endnote: 28 Une virgule a été ajouté ici dans la version imprimée. pour qu’il fût à gauche, il faudrait que la caractéristique sortît du cycle quand on la prolonge au delà de , c’est à dire que l’arc de caractéristique fût sous-tendu par l’arc ce qui est impossible puisque cet arc est sans contact
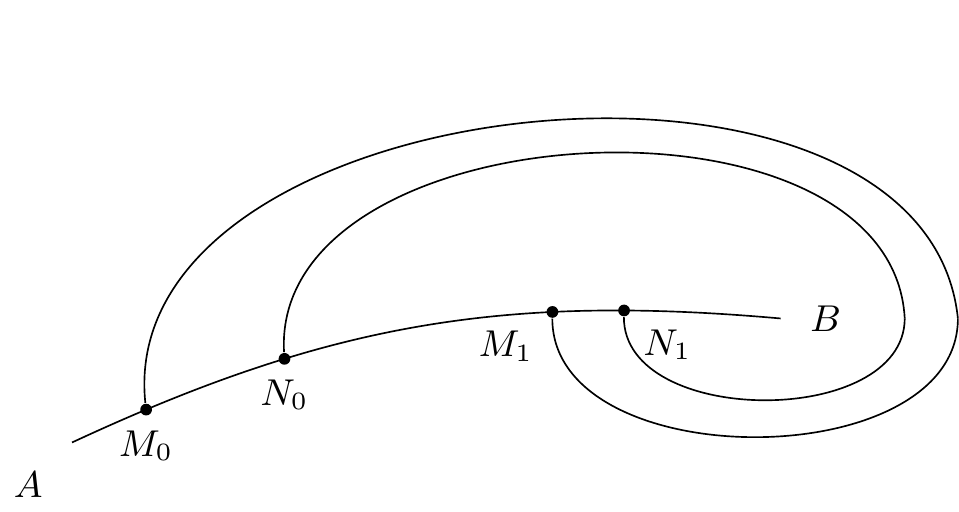
Etude de la courbe de conséquence :
Si l’on considère les quantités et comme les coordonnées d’un point, la loi de conséquence
représente une courbe. Cette courbe est comprise tout entière dans le carré :
1er cas :
A aucune valeur de comprise comprise entre et ne correspond de caractéristique allant passer par un col.
Dans ce cas la courbe de conséquence est continue; elle ne rencontre qu’en un point les parallèles aux axes; en suivant2929endnote:
29
Variante : “…aux axes; les points en suivant …”. la courbe dans un sens3030endnote:
30
Variante : “…la courbe dans un certain sens …”. convenable, on va constamment en s’éloignant des deux axes.
C’est dire que si est le carré (figure 11)3131endnote:
31
Variante : “(figure 7 11)”. :
la courbe présente des formes telles que :
Elle présentera3232endnote: 32 ”présentera” devient ”représentera” dans la version imprimée. la forme quand les valeurs et de correspondront à des cycles, pendant qu’aucune valeur de comprise entre et ne correspondront à un cycle.
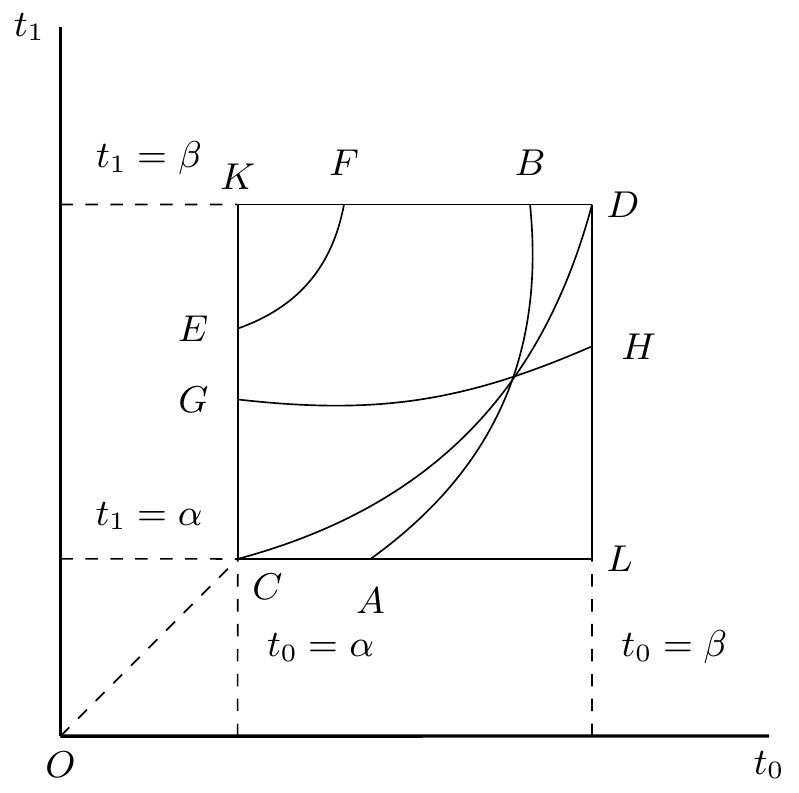
2eme cas :
A certaines valeurs , , etc de comprise entre et correspondent des caractéristiques allant passer par un col.3333endnote: 33 La version imprimée commence par une suppostion : “Supposons qu’à certaines valeurs …”.
Aux valeurs et correspondent des cycles; à aucune valeur intermédiaire ne correspond un cycle.3434endnote: 34 “Aux valeurs” devient “Que de plus aux valeurs” dans la version imprimée.
De tous les cols3535endnote: 35 Variante : “Nous supposerons d’abord que les branches de courbe De tous les cols…”. partent quatre branches de…3636endnote: 36 Il manque ici quatre pages (de la page 74 à la page 77 du manuscrit); ces pages correspondent à la fin du Chapitre V de la version imprimée, pages 259 à 261, comprenant quatre figures numérotées 12 à 15.
Chapitre VI : Théorie des cycles limites
D’après ce que nous avons vu plus haut, les caractéristiques peuvent se diviser en 4 catégories :
1° les cycles.
2° les spirales que l’on peut suivre indéfiniment dans les deux sens sans aboutir à un noeud, ou sans tourner autour d’un foyer, et sans revenir au point de départ.
3° les caractéristiques que l’on peut suivre indéfiniment dans un sens sans rencontrer un noeud ou se rapprocher d’un foyer; mais qui dans l’autre sens aboutissent à un noeud ou se rapprochent indéfiniment d’un foyer.
4° Celles qui aboutissent de part et d’autres à un noeud ou à un foyer.
D’après les3737endnote:
37
Variante : “De mem D’après”. mêmes principes, les demi caractéristiques se divisent en 4 catégories.
1° les cycles.
2° les demi-spirales, que l’on suit sur un arc infini sans arriver à un noeud ou à un foyer et sans revenir au point de départ.
3° Les demi caractéristiques qui aboutissent à un noeud.
4° Celles qui tournent indéfiniment autour d’un foyer.
D’après le théorème I, les demi caractéristiques de la catégories rencontrent certains cycles algébriques,
et par conséquent certains arcs algébriques sans contact en une infinité de points.
Soit un de ces arcs algébriques sans contact. Soit (figure 16)3838endnote:
38
Variante : “(figure 12 6)”. le point d’où est issue la demi caractéristique considérée. Soit le conséquent de et supposons que soit à droite de .
Soit le conséquent de , celui de , etc.
sera à droite de , à droite de , etc.
En général sera à droite de 3939endnote:
39
une virgule a été ajouté dans la version imprimée. et comme4040endnote:
40
une virgule a été ajouté dans la version imprimée. quelque grand que soit , est toujours sur l’axe ; tendra vers une limite quand augmentera indéfiniment. Soit cette limite.
Le conséquent de quand est indéfiniment grand et infiniment rapproché de . Donc est son propre conséquent; donc la caractéristique qui passe par est un cycle; nous l’appellerons cycle limite de la demi caractéristique donnée. On peut suivre sur la caractéristique qui passe par un arc assez grand pour se rapprocher autant l’on veut du point .
Soit un arc de la caractéristique qui passe par le point . Soit4141endnote:
41
Variante : ”On pourra prendre assez grand po Soit ”. un arc algébrique passant par .
On pourra prendre assez grand pour que l’arc de caractéristique issu de aille rencontrer .
Supposons par exemple que l’arc issu de aille
rencontrer en . L’arc issu de ira rencontrer en ,…, l’arc issu de en un point .
sera à droite de ,…, sera à droite de
. De sorte que la demi caractéristique donnée rencontrera en
une infinité de points , ,…, et que4242endnote:
42
Variante : “…,…, de telle et que …”. tendra vers quand augmentera indéfiniment.
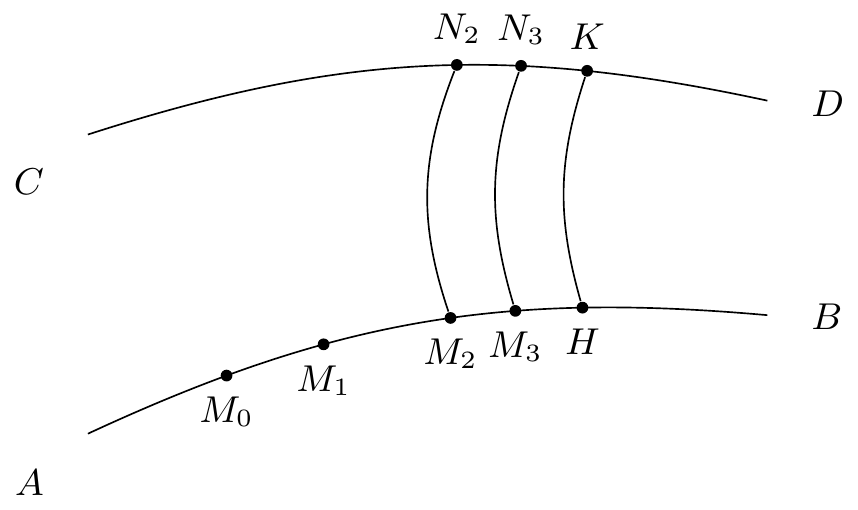
En résumé : toute demi caractéristique de la catégorie a un cycle limite.
Tout arc algébrique, si petit qu’il soit qui coupe ce cycle coupe la caractéristique en une infinité de points.
On peut trouver un point de la demi caractéristique qui soit aussi rapproché qu’on voudra d’un point quelconque de son cycle limite.
Soit (figure 17)4343endnote:
43
Variante : “(figure 13 7)”. un algébrique algébrique sans contact. Supposons qu’à aucun point situé entre et ne corresponde une caractéristique allant passe par un col; qu’au point corresponde un cycle limite et qu’à aucun point différent de et situé entre et ne corresponde un cycle limite. Toute caractéristique qui rencontre aura pour cycle limite le cycle qui passe par .
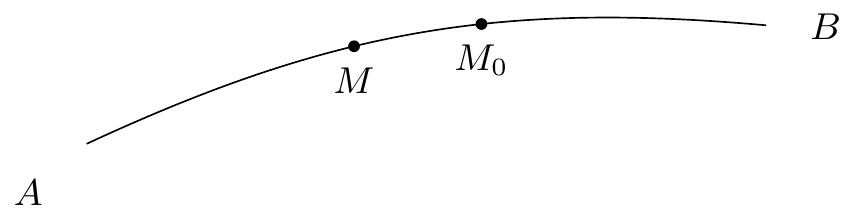
Si l’on considère un cycle limite (figure 18)4444endnote:
44
Variante : “(figure 14 8)”. qui ne passe par aucun col et qui passe par un point , on pourra mener par un arc algébrique assez petit pour
qu’il soit sans contact; pour qu’entre et ou entre et ,4545endnote:
45
La virgule n’apparaît pas dans la version imprimée. il n’y ait aucun point auquel corresponde une caractéristique passant par un col ou un cycle limite. Toutes les caractéristiques qui rencontrent ont alors pour cycle limite, de sorte que est le cycle limite de deux séries de caractéristiques situées l’une à l’intérieur du cycle, l’autre à l’extérieur.
Voyons ce qui se passe quand va passer par un col.
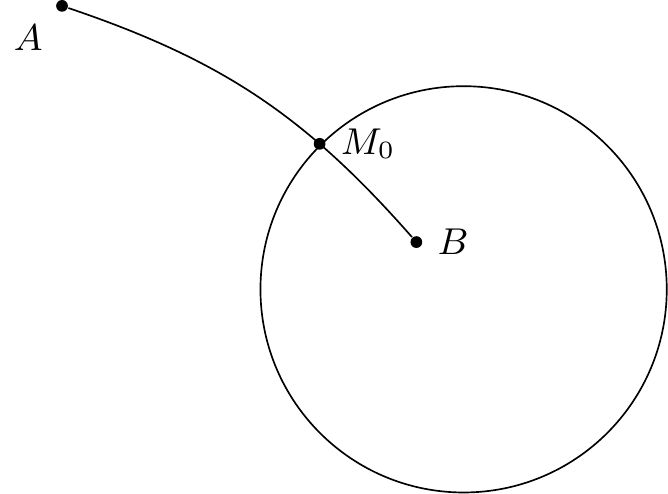
Soit le col, , , , les quatres branches de caractéristiques issues de ce col. Supposons que deux de ces branches, et par exemple aillent aboutir à un même point , de façon à former un cycle ; ce cycle sera toujours cycle limite de courbes telles que ; l’inspection de la figure le démontre (figure 19).4646endnote:
46
Variante : “(figure 15 9)”.
Considérons au contraire la courbe , il est aisé de voir
que, si les branches de courbe , ne vont pas aboutir en un même point ; le cycle n’est pas cycle limite de .
Si, au contraire, et vont se réunir en , a
pour cycle limite le polycycle

Théorème XV :
A l’intérieur et à l’extérieur d’un cycle limite quelconque, il y a toujours au moins un foyer ou un noeud.
Pour démontrer ce théorème, nous allons appeler
tangences d’un cycle les points où il touche un des grands cercles 4747endnote:
47
Variante : “ ”..
Les tangences seront directes, si dans le voisinage du point de contact, le grand cercle tangent reste à l’extérieur du cycle. Elles seront inverses dans le cas contraire.
Nous démontrerons ensuite les deux lemmes suivants.
Lemme I :
Si les points d’intersections de l’équateur avec le grand cercle , points que nous appellerons , sont tous deux à l’extérieur d’un cycle, l’excès du nombre des tangences directes de ce cycle sur le nombre de ses tangences inverses est de 2;
Si les points , sont tous deux à l’intérieur du cycle cet excès est de -2.
Si les points , sont l’un à l’extérieur, l’autre à l’intérieur, cet excès est de 0.
En effet on peut passer d’un cycle quelconque à un autre cycle également quelconque par voie de déformation continue, c’est à dire en passant du cycle à un cycle qui en diffère infiniment peu , et ensuite par une série de cycle4848endnote:
48
Variante : “…et de celui ci ensuite par une cycle série infiniment …”. infiniment peu différents les uns des autres, on arrivera à un cycle infiniment peu différent de .
Dans ces déformations successives, une tangence directe ne se transformera jamais en une tangence inverse
ni une tangence inverse en une tangence directe, car cela ne pourrait avoir lieu que si l’un des grands cercles 4949endnote:
49
Variante : “y ”. devenait osculateur à l’un des cycles ; dans ce cas, ce serait que deux tangences, l’une directe, et l’autre inverse seraient venues à se confondre; et dans ce cas elles disparaîtraient en général pour un des cycles infiniment voisins de .
L’excès qu’il s’agit d’évaluer dans ce lemme ne peut se modifier dans ces déformations continues du cycle que si deux des tangences viennent5050endnote:
50
Variante : “…si deux des tangencs venant viennent à se …”. à se confondre, puis à disparaître. Or cela peut arriver dans deux cas :
1° Quand l’un des cycles vient à passer par l’un des points , ; mais nous supposerons5151endnote:
51
Variante : “…des points , ; mais si l’on suppose nous supposerons : 1° que les points …”. : 1° que les points , sont tous deux à l’intérieur de et tous deux à l’intérieur de , 2° ou que les points sont tous deux à l’extérieur de et à l’extérieur de . 3° ou que soit à l’extérieur de et de pendant que est à l’intérieur de ces deux cycles; et par conséquent on aura pu toujours choisir la série des cycles qui permettent de passer du cycle au cycle , de telle sorte qu’aucun des cycles ne passe ni par , ni par .
2° Cela peut arriver encore si l’un des cycles devient osculateur à l’un des cercles Mais dans ce cas, c’est une tangence directe et une tangence inverse qui se confondent et disparaissent. L’excès à
évaluer n’est donc pas modifié.
Donc cet excès est le même pour et pour .
Mais supposons que soit un cycle convexe quelconque et le cycle donné.
L’excès en question sera de 2 pour si et sont à l’extérieur de ; il sera de s’ils sont tous deux à l’intérieur et de 0 s’ils sont l’un à l’intérieur et l’autre à l’extérieur.
L’excès en question sera donc pour , de 2, de -2 et de 0 dabs les mêmes conditions.
Le lemme est donc démontré.
Lemme II :
Si l’on parcourt un cycle de manière à avoir toujours l’intérieur à sa gauche et que l’on observe les variations du cœfficient angulaire , on observera qu’à chaque tangence directe, 5252endnote: 52 “” devient “” dans la version imprimée. sautera de à 5353endnote: 53 Variante : “…sautera de à + …”. si l’on est dans le premier hémisphère, de à 5454endnote: 54 Variante : “…le premier hémisphère, et de + ”. si l’on est dans le second hémisphère et que c’est le contraire pour les tangences inverses.
Démonstration du théorème :
Supposons d’abord que le cycle limite considéré soit tel que les deux points et soient d’un même côté que nous appellerons l’extérieur du cycle.
Soit le nombre des noeuds et des foyers contenus à l’intérieur du cycle, le nombre des noeuds et des foyers situés à l’extérieur du cycle, et le nombre
des cols situés à l’intérieur et à l’extérieur du cycle. On a
Le cycle coupe l’équateur en un certain nombre de points, de telle façon qu’on peut le partager en un certain nombre de cycles secondaires, situés les uns tout entiers dans le premier hémisphère, les autres tout entiers dans le second hémisphère, et formés à l’aide d’arcs du cycle primitif et d’arcs de l’équateur.
Supposons pour fixer les idées que le cycle donné soit le cycle qui coupe l’équateur aux points , , , (figure 20)5555endnote:
55
Variante : “(figure 16 20)”.. Le cycle se décompose en trois cycle secondaires
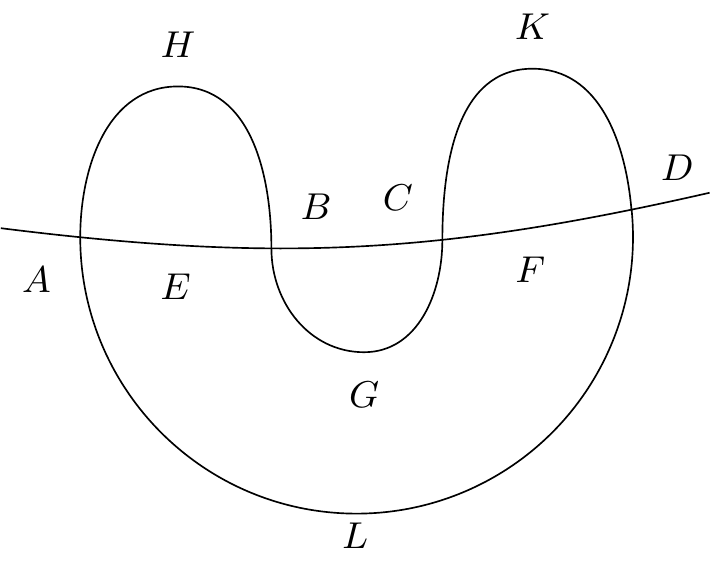
Or d’après le théorème IV, on a
Soit maintenant , , , le nombre des tangences directes des arcs , , , 5757endnote: 57 ”, , , ” devient ”, , , , ” dans la version imprimée., , , , le nombre de leurs tangences inverses, soit et 5858endnote: 58 Variante : “…soit et et ….”. le nombre des fois que saute de à quand on parcourt les arcs et , et le nombre de fois que saute de à quand on parcourt les arcs et , on a, en vertu du lemme II et en remarquant que tout le long du cycle donné on a
d’où
or d’après le lemme I
On a donc aussi :
d’où
C.Q.F.D.
Dans le cas où les points , sont de part et d’autre du cycle, la difficulté est facile à tourner. En effet, on trouvera toujours sur la sphère5959endnote: 59 Variante : “…on trouvera toujours sur l’équateur la sphère …”. deux points diamétralement opposés qui soient d’un même côté du cycle, et il suffira d’un changement de variables6060endnote: 60 Variante : “…d’un changement linéaire de variable …”. pour retomber sur le cas précédent. Si l’on ne trouve pas sur la sphère6161endnote: 61 Variante : “…Si l’on ne trouve pas sur l’équateur la sphère …”. deux points diamétralement opposés qui soient d’un même côté du cycle, c’est que les points du cycle sont deux à deux6262endnote: 62 Variante : “…c’est que le cycle passe par deux points les points du cycle sont deux à deux …”. diamétralement opposés, c’est à dire que le cycle6363endnote: 63 Variante : “…c’est à dire qu’il que le cycle est …”. est symétrique à lui-même par rapport au centre de la sphère, et alors le théorème est évident par lui-même.
Théorème XVI :
Un cycle algébrique qui passe par tous les noeuds et par tous les foyers rencontre tous les cycles limites.
En effet, soit un cycle limite quelconque, il contient certains noeuds et certains foyers à son intérieur, certains noeuds et certains foyers à l’extérieur.
Il y a donc des points du cycle algébrique donné qui sont à
l’extérieur de , et d’autre qui sont à l’intérieur, c’est à dire
que le cycle algébrique donné rencontre .
C.Q.F.D.
Corollaire :
Tout cycle algébrique qui passe par tous les noeuds et par tous les foyers, rencontre toutes les caractéristiques.
Théorème XVII :
Les cycles limites sont en nombre fini, pourvu qu’aucun d’eux ne passe par un col.
En effet faisons passer un cycle algébrique par tous les noeuds et par tous les foyers. Soient6464endnote: 64 Variante : “En effet Soient :…”. :
les équations de ce cycle .
Ce cycle rencontrant tous les cycles limites, aurait une infinité de points d’intersection avec ces cycles limites, si ceux-ci étaient en nombre infini. Il y aurait donc un point de ce cycle autour duquel ces points d’intersections seraient infiniment rapprochés, c’est à dire que si
est la loi de conséquence d’un certain arc sans contact du cycle , il y aura une certaine valeur
de , telle que 6565endnote:
65
Une note est présente dans la marge : “1b (ou 16) Brabant”. variant de à , devienne un nombre infini de fois égal à .
Mais si ne correspond pas à une caractéristique passant par un col, est holomorphe pour , et on ne peut donc avoir une infinité de fois ( variant de à ) :
Cela ne peut arriver non plus si ne correspond pas à un cycle limite.
Donc on ne peut avoir une infinité de cycles limites que si l’un d’eux vas passer par un col.
Théorie des anneaux limites :
Soit encore un cycle algébrique passant par tous les noeuds et par tous les foyers. On peut y découper6666endnote:
66
Variante : “On peut le diviser en y découper un certain …”. un certain nombre d’arcs sans contact contenant tous les points qui correspondent à des cycles limites et ne contenant aucun des points qui correspondent à des caractéristiques passant par des cols.
Soit la loi de conséquence de l’un ces arcs6767endnote:
67
Variante : “…la loi de conséquence de cet arc l’un de ces arcs, …”., et supposons que l’on fasse varier depuis jusqu’à ; que les points , aient deux conséquents , . Soit le point de l’arc sans contact qui correspond à . Supposons que l’on considère6868endnote:
68
Variante : “…Supposons que l’on représente par considère le point …”. le point de la sphère qui se trouve sur la caractéristique qui passe par 6969endnote:
69
“” devient “” dans la version imprimée. et qui est séparé de par un arc
de caractéristique, et qu’on fasse correspondre à ce point un point du plan qui ait pour coordonnées et (figure 21)7070endnote:
70
Variante : “(figure 17 21)”.
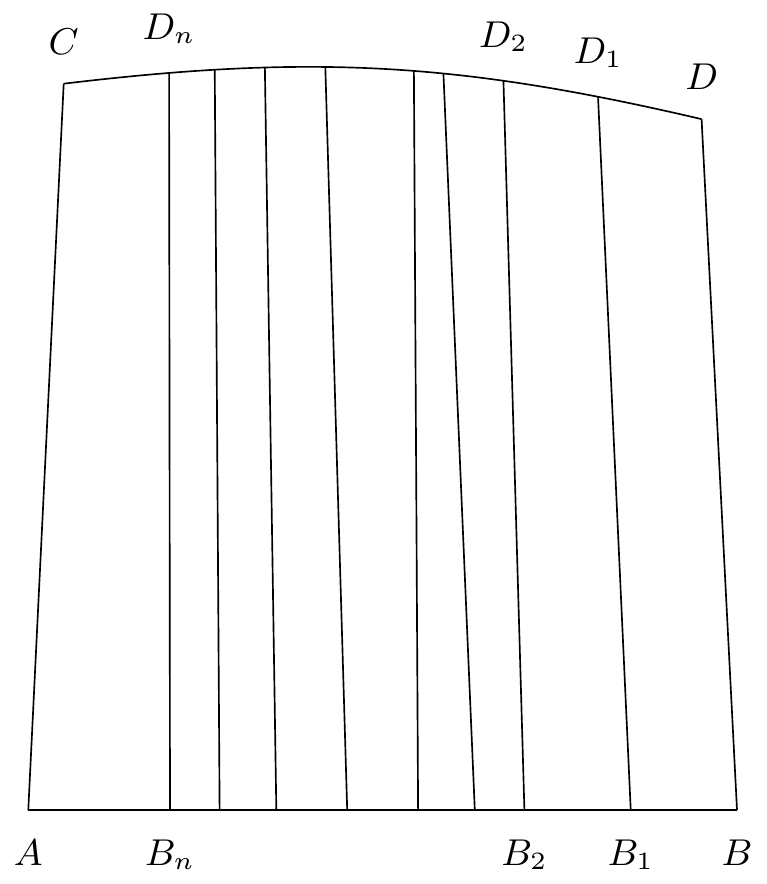
A l’arc sans contact correspondront :
1° le segment de la droite comprit entre les points
2° un certain arc de courbe , défini par l’équation
étant la longueur de la caractéristique passant par qu’il faut parcourir avant de rencontrer de nouveau l’arc sans contact.
Un point quelconque de l’arc sans contact sera représenté par un point du segment7171endnote:
71
Variante : “…par un point deu l’ar segment …”. et par un point de l’arc . Tout arc de courbe allant de à représente un cycle; ce cycle sera sans contact, si l’arc de courbe n’est tangent à aucune des droites
Or il est clair qu’on peut joindre par des droites, et , 7272endnote:
72
“” devient “” dans la version imprimée. et 7373endnote:
73
Variante : “…joindre par des droites, et , et , puis …”., puis sillonner le quadrilatère mixtiline par des arcs de courbes qui ne sont tangents à aucune des droites et qui ne se coupent en aucun point.
Conséquence :
Autour d’un cycle limite quelconque se trouve une région annulaire qui est limitée par deux cycles sans contact que nous appellerons cycles frontières et qui est sillonnée de cycles sans contact qui ne
se coupent en aucun point.
Ces régions annulaires s’appelleront anneaux limites et seront en nombres fini.
Autour des noeuds et des foyers, on peut également tracer une série de cycles sans contact s’enveloppant mutuellement, de sorte que les noeuds et les foyers ont aussi leurs anneaux limites.
Nous avons implicitement supposé qu’aucun cycle limite ne passait par un col,7474endnote:
74
Variante : “…cycle limite ne passait par un noeud col, car nous …”. car nous avons envisagé sur le cycle algébrique des arcs sur lesquels se trouvaient tous les points auxquels correspondent des cycles limites, et ne se trouvait aucun des points auxquels correspondent des caractéristiques passant par des cols.
Supposons maintenant qu’un cycle limite aille passer par un col, nous savons que deux cas peuvent se présenter :
1° Une pareil caractéristique n’est cycle limite7575endnote:
75
Variante : “…Une pareil cycle caractéristique n’est limite cycle limite …”. que des caractéristiques qui lui sont suffisamment voisines et qui sont situées à l’intérieur du cycle (voir figure 19). Dans ce cas, on découpera sur le cycle un arc sans contact limité au point qui correspond au cycle limite qui passe par un col, et ne contenant aucun autre point correspondant à une caractéristique passant par un col, et, raisonnant comme dans le cas général, on fera voir que le cycle qui passe par un col, a également un
anneau limite, mais dont il est lui-même le cycle frontière.
2° Les cycles , (figure 19) sont cycles limites des caractéristiques situées à l’intérieur de ces cycles, pendant que le polycycle est cycle limite des caractéristique extérieures.
Raisonnant comme dans le premier cas particulier, on verrait que chacun de ces trois cycles a un anneau limite, dont il est lui-même le cycle frontière, de sorte que ces trois anneaux limites forment par leur juxtaposition une seule région annulaire.
Régions interannulaires :
Les cycles frontières divisent la sphère eu deux catégories de régions : 1° les anneaux limites que nous venons d’étudier. 2° les régions interannulaires.
Un mobile parcourant une caractéristique d’une vitesse uniforme et partant d’un point situé dans une région interannulaire, ira après un temps fini traverser un cycle frontière pour passer dans un anneau limite.
Car les régions interannulaires ne contiennent ni noeud, ni foyer, ni aucun point des cycles limites.
Je dis que les régions interannulaires sont commes les anneaux limites sillonnées par des cycles sans contact. En effet supposons pour fixer les idées qu’une région interannulaire soit limitée par trois
cycles frontières , , et divisée en deux parties, sillonnées la première par des caractéristiques allant de en , la seconde par des caractéristique allant de en . Les deux parties de la région devront être séparées par une caractéristique allant passer par un col (figure 22).7676endnote:
76
Variante : “(figure 18 22)”. Soient , , , les quatre branches de caractéristiques issues de .7777endnote:
77
La forme de la figure est différente dans la version imprimée, cette dernière ayant une forme arrondie à la place d’une forme en huit.
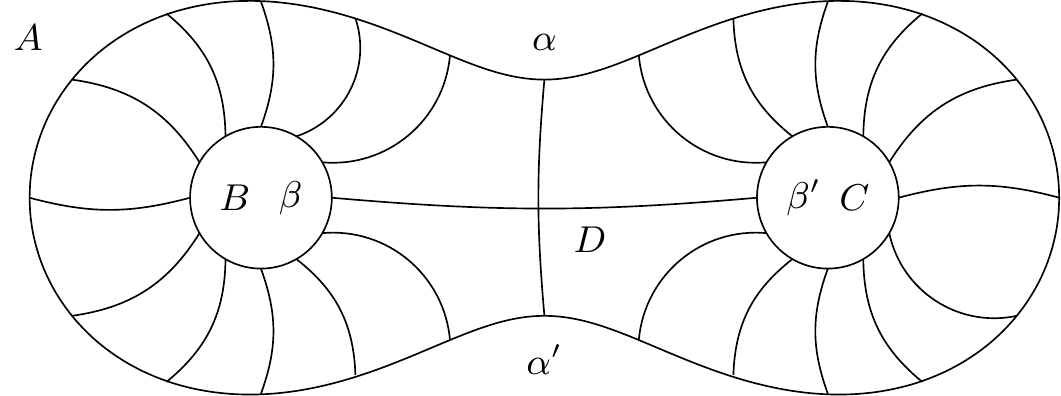
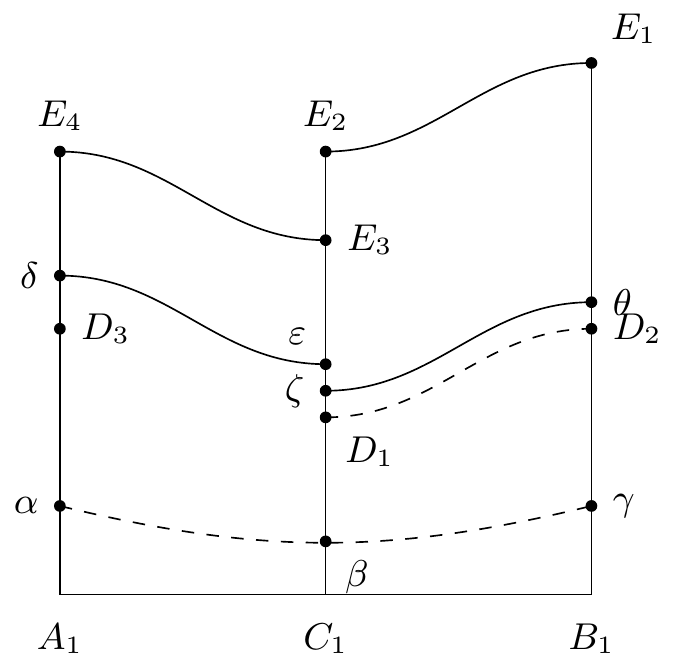
Soit un paramètre quelconque définissant un point du cycle . Soit , un point d’une caractéristique issue de , et l’arc de caractéristique qui sépare , de . Représentons le point de la sphère , par le point du plan dont les coordonnées sont et . La droite () (figure 23)7878endnote: 78 Variante : “(figure 19 23)”. représentera le cycle ; et représenteront le point , représentera le point ; les arcs , représenteront respectivement les cycles et ; , , représenteront le point ; et représenteront ; et représenteront . D’ailleurs on aura
Les arcs de la courbe , , où l’on a :
représentent des cycles et ces cycles seront sans contact si les arcs , , n’ont pas de tangente parallèle à l’axe des . Or il est clair qu’on peut sillonner le polygone mixtiligne d’arcs satisfaisant à cette condition. Donc on peut sillonner la région interannulaire de cycles sans contact ce qui permet d’énoncer le théorème suivant.
Théorème XVIII :
7979endnote: 79 Le manuscrit comporte une note marginale en crayon de couleur bleue de main inconnue, sans doute du compositeur: “ital”, accompagnée d’une accolade sur le côté du théorème.Il existe toujours un système topographique formé de cycles sans contact, de polycycles sans contact et de cycles limites. Ce système topographique sillonne tout la surface de la sphère. Les fonds et ses sommets sont les noeuds et les foyers de l’équation donnée. Les cols sont les cols de l’équation donnée.
La connaissance de ce système topographique permet de discuter complètement les formes affectées par les courbes que définit l’équation différentielle donnée. On le comprendra mieux d’ailleurs par les exemples qui vont suivre.
Chapitre VII : Exemples de discussions complètes
1er exemple :
Soit (figure 24) l’équation :
On peut remarquer d’abord que les courbes , , qui sont l’une , l’autre ne se coupent en aucun point ni en dehors de l’équateur ni sur l’équateur.
Si de plus et sont les termes du second degré de et de on a :
L’expression ne s’annule que pour . Donc l’équation ne présente aucun point singulier en dehors de l’équateur, et sur l’équateur même elle en a deux qui sont à l’intersection de l’équateur avec le grand cercle , et qui sont évidemment des noeuds.
L’équateur passant par tous les points singuliers rencontre tous les cycles limites, mais comme c’est une caractéristique, et qu’elle ne passe par aucun col, elle ne peut rencontrer aucune autre caractéristique en aucun autre point qu’aux deux
noeuds, et ; elle ne rencontre donc aucun cycle limite, donc il n’y a pas de cycle limite. Donc toutes les caractéristiques partent de pour aller aboutir en .
La figure 24 se présente la projection stéréographique du premier hémisphère. est l’équateur, sont les noeuds; , sont des caractéristiques.
2ème exemple :
Soit (figure 25) l’équation :
Ici encore les courbes , ne se coupent pas mais l’expression se réduit à :
de sorte qu’elle s’annule pour :
C’est dire :
1° qu’en dehors de l’équateur, il n’y a pas de point singulier.
2° que sur l’équateur, il y a 6 points singuliers dont 4 noeuds et deux cols.
En posant :
l’équation devient :
Faisons successivement , , , le coefficient de dans le dénominateur de sera toujours négatif. Considérons la différentielle du dénominateur de , par rapport à ; elle sera :
Négative pour
Positive pour
Négative pour
Donc les points , sont des noeuds, le point est un col.
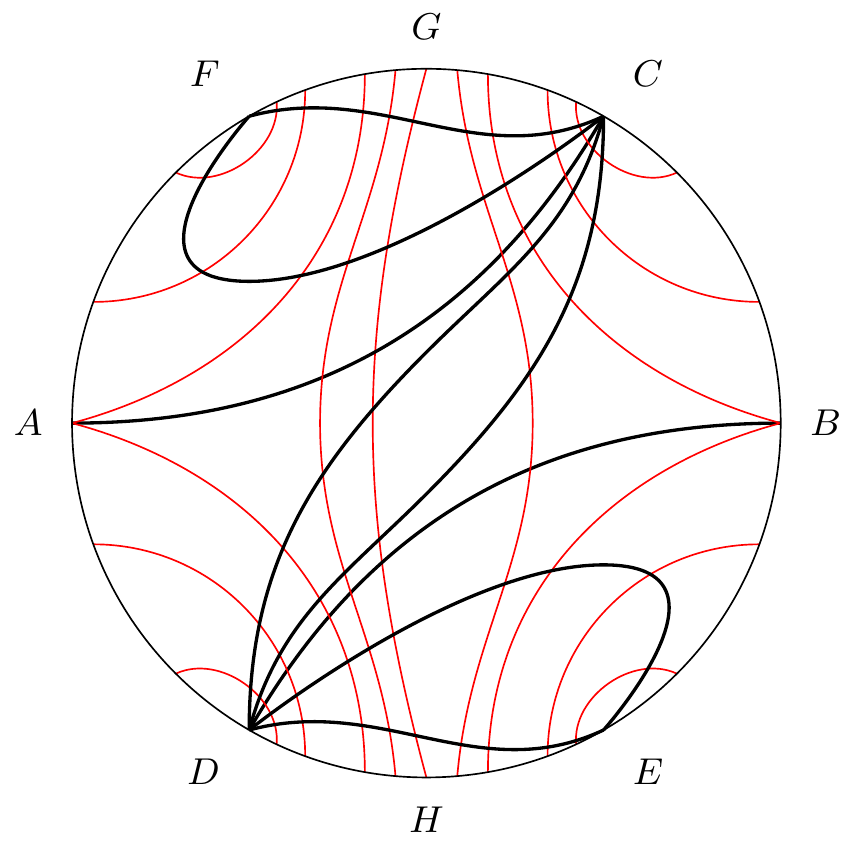
La figure représente encore la projection stéréographique du premier hémisphère; et sont les deux cols, , , , les quatre noeuds.
Le système topographique des cycles sans contact a pour fonds et pour sommets , , , , pour col et .
Considérons maintenant le grand cercle :
En aucun point de ce grand cercle qui se projette en on n’a :
ni par conséquent . C’est donc un cycle sans contact. Donc si est un fond du système topographique des cycles sans contact, est également un fond pendant que et sont des sommets.
Les lignes tracées en traits ponctués sur la figure
représentent alors le système topographique des cycles sans contact. D’ailleurs on ferait voir comme dans le 1er exemple, qu’il n’y a pas de cycle limite. Les caractéristiques issues de iront donc aboutir soit en , soit en , et la région occupée par les caractéristiques allant de en sera séparée de celle qui est occupée par les caractéristiques allant de en , par une caractéristique allant de en . Il y a donc une caractéristique allant de en s’il y en a allant de en . Dans ce cas il y en a également une allant de en
Nous nous trouvons donc en présence de deux hypothèses :
| 1er hypothèse | 2ème hypothèse | |
|---|---|---|
| Une infinité de caractéristiques allant : | de en | de en |
| de en | de en | |
| de en | de en | |
| Une caractéristique allant : | de en | de en |
| de en | de en |
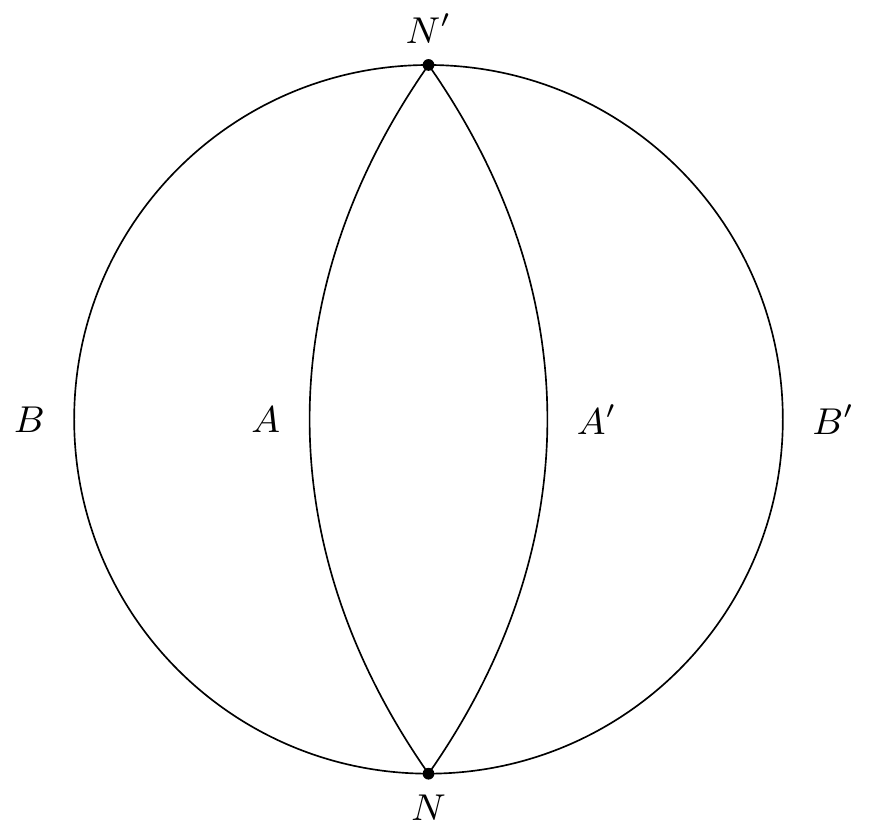
Pour décider entre ces deux hypothèses, remarquons que l’arc de grand cercle qui va de en est un arc sans contact. La caractéristique issue du point ne peut donc le couper. Elle est donc tout entière dans l’un des deux quarts de sphère , .8080endnote: 80 Une note marginale de la main de Poincaré accompagne la figure: “Voir les figures 21, 22, 23, 24 à plus grande échelle aux pages 103, 104 et 105”. Il s’agit, après une opération de rénumeration réalisée sans doute par Poincaré des figures 25 à 28.
Dans le voisinage du point , l’équation différentielle s’écrit :
représentant une série commençant par les termes du quatrième degré en et en ; d’où nous tirons :
étant une fonction holomorphe en .
Donc dans le voisinage du point , la caractéristique qui passe par ce point, passe par des points correspondant à , c’est à dire que la caractéristique est dans le quart de sphère . Elle est donc tout entière dans ce quart de sphère; elle ne peut donc aboutir au noeuds ; elle aboutit donc au noeuds . C’est la première hypothèse qui doit être adoptée et les caractéristiques présentent les formes représentées en trait plein sur la figure
3ème exemple :
Soit (figure 26) l’équation :8181endnote: 81 Variante barrée: “ ”.
Il n’y a qu’un point singulier dans chaque hémisphère. C’est le point qui est un foyer.
Il y a aucun point singulier sur l’équateur qui
est une caractéristique et qui est par conséquent un cycle limite.
Considérons le système topographique des cercles qui ont leur centre à l’origine, c’est à dire des cycles :
La courbe des contacts de ce système topographique est :
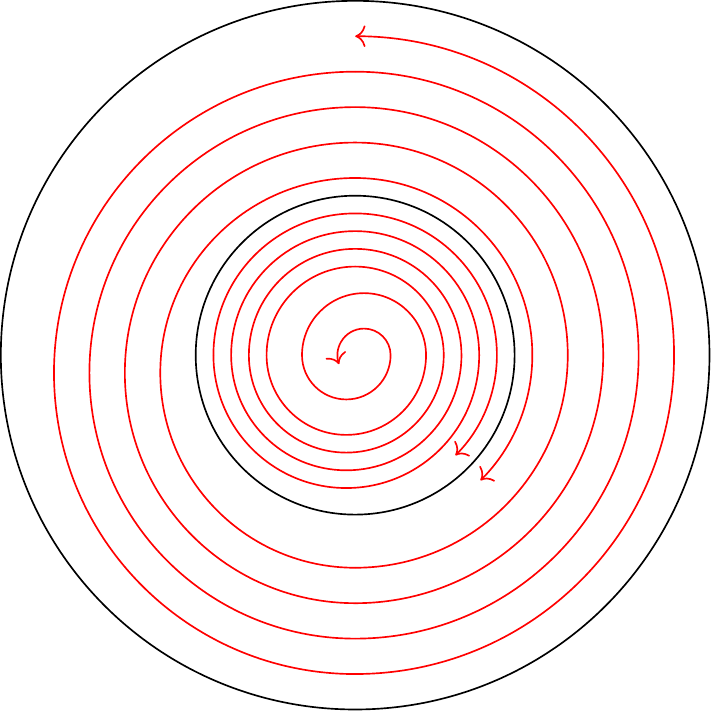
c’est à dire que tous ces cercles sont des cycles sans contact, excepté le cercle de rayon qui est un cycle limite. Il n’y a pas d’autre cycle limite. Le système des caractéristiques présente donc l’aspect de la figure 26 où les traits tels que () représentent les cycles limites, et les traits tels que (→) les caractéristiques.8282endnote: 82 La légende est adaptée à la figure de la transcription (les figures à grandes échelles sont légèrement différentes de celles illustrant les exemples). Dans le manuscrit, les deux cycles limites sont indiqués dans la figure 26 par deux cercles dont la circonférence est hachée. La figure du manuscrit n’est pas colorée.
4ème exemple :
Soit (figure 27) l’équation :
On voit qu’il y a trois points singuliers :
1° Le point ,
2° Les points et d’intersection des cercles :
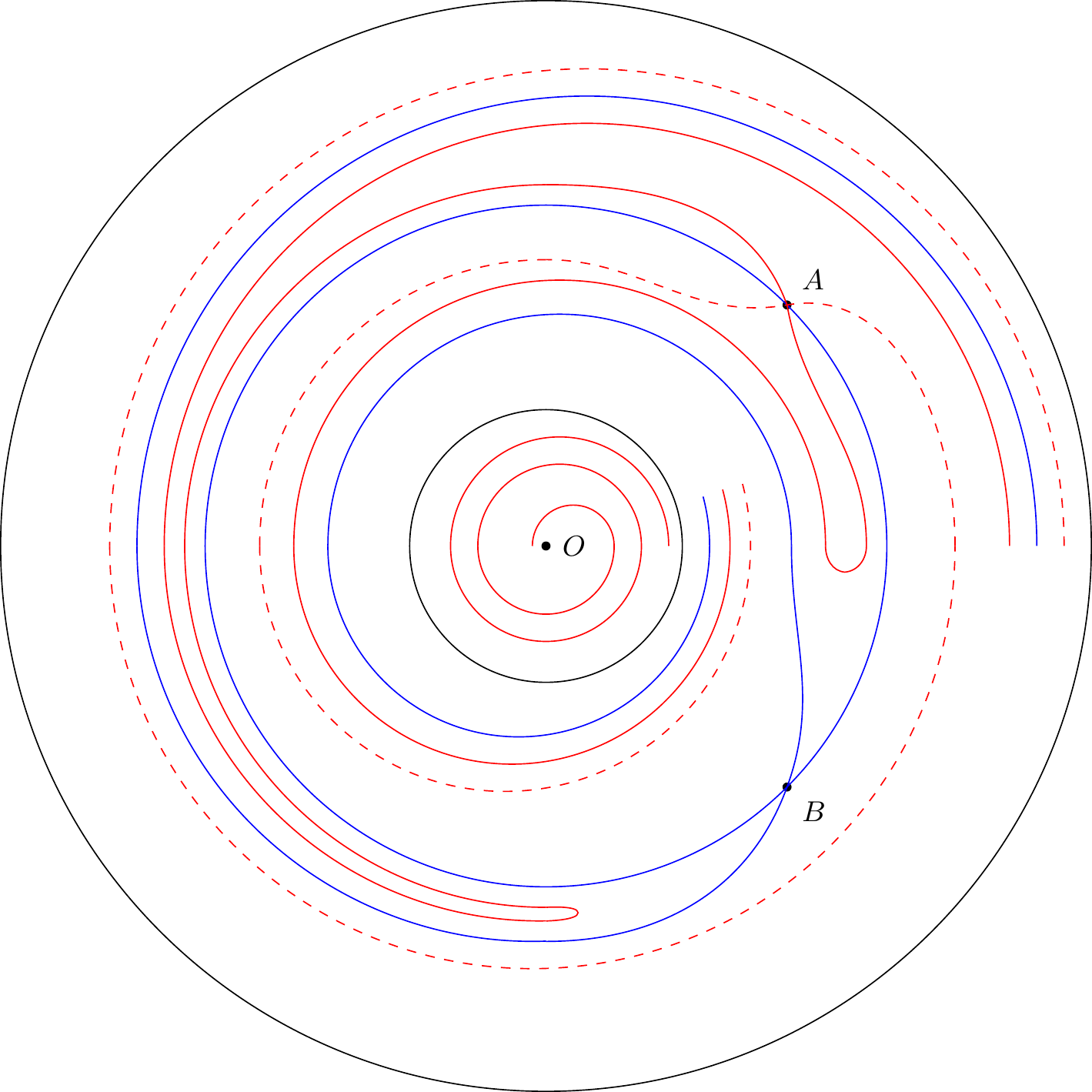
Le point est un foyer, le point est un noeud, le point est un col. On verrait comme dans l’exemple précédent que l’équateur est un cycle limite; que les cercles qui ont l’origine pour centre sont des cycles sans contact, excepté les cercles :
qui sont des caractéristiques.
Le premier qui ne passe par aucun point singulier est un cycle limite, le second passe par un noeud et par un col.
Il y a donc trois catégories de caractéristiques : les premières tournent autour du foyer (figure 27) et ont pour cycle limite
les secondes aboutissent au noeud et ont pour cycle limite
les troisièmes aboutissent au noeud et ont pour cycle limite l’équateur.
Comme caractéristiques exceptionnelles on a :
1° l’équateur
2° le cercle
3° le cercle
4° une caractéristique partant du col et ayant pour cycle limite l’équateur.
5° une caractéristique partant du col et ayant
pour cycle limite .
Un point mobile qui si représente le temps se meut d’après la loi :
ne pourra sortir du cercle
s’il se trouve à l’intérieur de ce cercle.
5ème exemple :
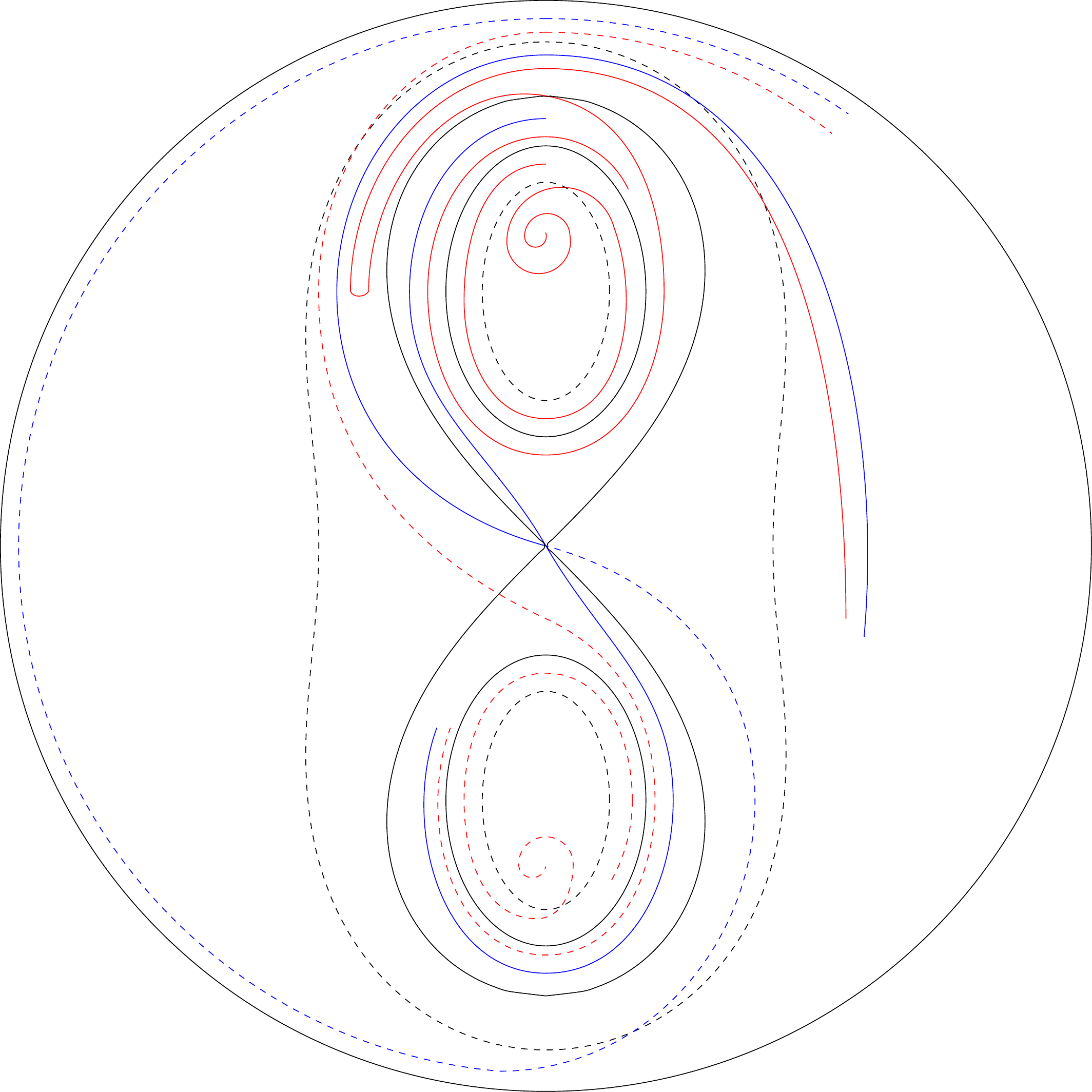
Soit (figure 28) l’équation :
où :
Les points singuliers nous sont donnés par les équations :
d’où
.
Ils sont donc au nombre de trois, dans chaque hémisphère, à savoir :
1° deux foyers : ,
2° un col :
Si nous considérons les courbes
leurs contacts nous seront donnés par l’équation :
Or
l’équation précédente devient donc :
où
Ma la courbe est elle-même une des courbes
Toutes les courbes sont donc formées de cycles sans contact excepté la courbe qui est formée de cycles limites.
L’équateur est aussi un cycle limite.
Il reste à construire les courbes algébriques
Pour , la courbes est entièrement imaginaire.
Pour , elle se réduit aux deux points singuliers , .
Pour elle se compose de deux cycles. Il en est ainsi en particulier de la courbe , qui se compose de deux cycles limites.
Pour , elle se réduit à un polycyle ayant un point double à l’origine.
Pour elle se compose d’un seul cycle.
Le système des caractéristiques présente donc la forme qui est indiquée par la figure .8484endnote:
84
Les pages suivantes du manuscrit (page 103 à 105) sont consacrées aux représentations à plus grandes échelles des figures 25 à 28. Une note est écrite à côté de la figure 28 : “Manque la fig 28 (petite échelle)”.
Chapitre VIII : Recherche des cycles sans contact
La facilité avec laquelle se discutent complètement les exemples précédents est due à deux causes. En premier lieu, les cycles limites étant algébriques, le système topographique des cycles sans contact et des cycles limites est lui-même algébrique, en second lieu la forme même de l’équation différentielle permet de trouver immédiatement ce système topographique; mais il est évident que cela n’aura pas lieu en général.
Quand les cycles limites ne sont pas algébriques, une discussion complète est évidemment impossible; car on ne pourra jamais trouver en termes finis l’équation des cycles limites. Mais on peut arriver à diviser la sphère : 1° en régions acycliques où l’on est certain de n’avoir aucun point d’aucun cycle limite; 2° en régions monocycliques, où se trouvent tous les points d’un des cycles limites et où l’on a aucun des points d’aucun autre cycle limite.
Une pareille séparation des cycles limites sera toujours possible quand les cycles limites seront en nombre fini.
Dans ce qui va suivre, nous supposerons : 1° qu’il n’y a que deux points singuliers situés en dehors de l’équateur
et que par conséquent, ces deux points sont des foyers ou des noeuds. 2° que ces deux points ont pour coordonées :
Dans les cas où il y aurait plus de deu points singuliers, la discussion serait plus longue et plus compliqué.
Dans le cas auquel nous nous restreignons, il n’y a qu’un nombre fini de cycles limites de sorte que la séparation de ces cycles est toujours possible.
Nous ne considérerons que ce qui se passe dans le 1er hémisphère. En effet, tout se passe de même de l’autre côté de l’équateur qui est un général un cycle limite.
Nous diviserons cet hémisphère :
1° en régions acycliques qui ne peuvent être traversées par aucun cycle limite.
2° en régions monocycliques qui contiennent un cycle limite tout entier et ne sont traversées par aucun autre.
3° en région cycliques qui contiennent certainement un cycle limite tout entier et sont peut-être traversées par un ou plusieurs autres cycles limites.
4° en régions douteuses, qui contiennent peut-être un cycle limite tout entier, peut-être plusieurs, et qui peut-être ne sont traversées par aucun cycle limite.
On poussera la discussion en cherchant à étendre les région acycliques de façon à resserrer les cycles limites dans des régions monocycliques de moins en moins étendues, et à faire disparaître les régions cycliques et les régions douteuses. On pourra, si l’on veut, terminer la discussion, quand il n’y aura plus que des régions acycliques et monocycliques; on pourra aussi la pousser plus loin, de façon à étendre encore les régions acycliques et à y tracer un plus grand nombre de cycles sans contact.
Méthode générale :
Considérons une fonction algébrique :
1° qui reste toujours finie et déterminée ainsi que ses dérivées quand et prennent des valeurs réelles et finies et devient infinie quand ou sont infinis.
2° qui soit nulle pour et positive toutes les fois que ou sont différents de .
3° dont les dérivées du premier ordre ne s’annulent à la fois que si .
4° telle que pour on ait l’inégalité
5° telle que la courbe :
ne coupe pas l’équateur.
L’équation :
où est une constante quelconque, représente un système topographique ayant pour sommet l’origine et dont l’équateur est un cycle.
La courbe des contacts dont l’équation est :
ne coupe pas l’équateur, en vertu de la 5e condition et a à l’origine un point isolé, en vertu de la 4e condition.
Les cycles sont donc sans contact si est très petit et s’il est très grand. Faisons varier depuis jusqu’à et supposons par exemple que pour
le cycle soit sans contact
le cycle ne soit pas sans contact
le cycle soit sans contact
le cycle ne soit pas sans contact
le cycle soit sans contact
Alors les régions de la sphère définies par les inégalités :
seront acycliques; les régions définies par les inégalités :
seront douteuses.
1er Problème :
Reconnaître si une région douteuse est cyclique.8585endnote: 85 Ce 1\uper problème était présenté d’abord comme le 2\upe problème (cette mention étant barrée). Aux pages 109–110 du manuscrit se trouve ce que Poincaré presentait d’abord comme le 1\uper problème; nous le transcrivons ainsi : “1\uper Problème : Reconnaître si une région douteuse est cyclique. Supposons que l’un des cycles qui forment la courbe des contacts entoure l’origine et soit situé tout entier dans une région douteuse, je dis que cette région est cyclique.En effet envisageons le système topographique des cycles sans contact et des cycles limites, système topographique dont le théorème XVIII a démontré l’existence, et envisageons le lieu des points de contact des cycles de ce système avec les cycles ; ce lieu est une courbe continue qui passe par l’origine et va couper l’équateur. Aux points où elle coupe la courbe il y a contact entre une caractéristique et l’un des cycles ; ce cycle n’est donc pas sans contact, c’est donc un cycle limite. Mais si un des cycles M1 qui forment cycle faisant partie de la courbe entoure l’origine, il sera forcément coupé par la courbe qui va de l’origine à l’équateur; et par conséquent par un cycle limite; si donc il est tout entier dans une région douteuse cette région sera cyclique. C.Q.F.D. 2\upe Problème. Reconnaître si une région cyclique est monocyclique.”
Pour cela, nous allons donner un moyen de reconnaître si dans une région douteuse passe un nombre pair ou impair de cycles limites. Il est clair que si l’on trouve que le nombre des cycles limites qui traversent une région douteuse est impair, c’est que cette région est cyclique. Pour résoudre le problème que nous nous
sommes proposé, il est nécessaire d’introduire une notion nouvelle :
Soit un arc d’un cycle sans contact; soit un arc du grand
cercle (fig 29). Soit la portion de cet arc qui
est situé à l’extérieur du cycle , la portion qui est située
à l’intérieur; la portion de l’arc qui serait à la droite
d’un observateur ayant les pieds sur la sphère en et regardant du
côté de ; la portion qui serait à la gauche de cet
observateur. Nous dirons que le cycle est positif par rapport à
l’arc de grand cercle quand la caractéristique qui passe en
est située dans l’angle , en par exemple, et qu’il est
négatif, quand cette caractéristique est située dans l’angle , en
par exemple.
Ceci posé, remarquons que si l’on fait varier le cycle , ce cycle change de signe : 1° toutes les fois qu’il devient un cycle limite. 2° toutes les fois que est tangent à .
Maintenant nous sommes en état de résoudre le problème proposé. A cet effet, considérons la région douteuse comprise entre les cycles
Soient et les points où l’arc de grand cercle rencontre ces cycles. Soit le nombre des cycles limites compris dans la région douteuse, soit le nombre des contacts du grand cercle compris entre et ; soit un nombre qui est pair si les cycles , sont de même signe, impair dans le cas contraire; soit le nombre de fois que les cycles sans contact du système topographique défini au théorème XVIII changent de signe quand on passe du cycle au cycle ; on aura :
d’où
ce qui permet de voir si le nombre des cycles limites est pair ou impair.
2e problème
Reconnaître si une région est monocyclique.
Pour résoudre ce problème, appuyons-nous sur le théorème suivant.
Théorème XIX :
Si l’on pose8686endnote: 86 Une note est présente dans la marge :“Rochereau”.
et que l’équation différentielle devienne
si est une fonction quelconque de n’ayant qu’une valeur finie pour chaque valeur finie de ; entre deux cycles limites quelconques il y a toujours des points où :
ou bien où :8787endnote: 87 “” devient “” dans la version imprimée.
Soit en effet une certaine valeur de , et les valeurs de qui correspondent aux points
d’intersection des deux cycles limites considérés et de l’arc de grand cercle
Considérons la fonction :
et voyons comment elle varie quand varie de à . Il est clair qu’elle varie d’une façon continue, qu’elle reste finie et qu’elle revient à la même valeur. Elle passe donc par un maximum et pour une certaine valeur de correspondant à des valeurs et de et , on aura :
ou
Donc si l’on considère comme une constante égale à , et qu’on fass varier depuis jusqu’à la fonction
deviendra infinie ou passera par un maximum, c’est à dire que l’on
aura :8888endnote:
88
Le manuscrit porte un note
marginale de main inconnue : “Brabant”.
ou bien
ou bien
ou bien
C.Q.F.D.
Théorème XIX généralisé :
Si et sont deux fonctions continues de et de
telles qu’à chaque système de valeurs de et de corresponde un système de valeurs de et de et un seul et qu’à chaque système de valeurs de et corresponde un système de valeurs de et de et un seul.
Si l’on pose ,
Si après cette transformation l’équation devient :
dans la région comprise entre deux cycles limites, il y aura toujours des points, tel que :
ou bien :
En effet, soient et les deux cycles limites donnés. Supposons qu’en aucun point de la région comprise entre ces deux cycles limites on n’ait ; je dis qu’il y aura dans cette région des points où l’on aura :
En effet soit un point du cycle , et soit la valeur correspondante de la fonction ; l’arc de courbe
qui passe en , va couper le cycle en un point , car s’il ne coupait pas le cycle , il ne pourrait sortir de la région qu’en coupant qu’en recoupant le cycle ; il devrait donc, dans cette région être tangent à une caractéristique (en vertu dh théorème X). Or cela est impossible puisqu’on a supposé que dans la région on n’a pas :
Soient donc et les valeurs de qui correspondent aux points et .
Quand le point fera le tour du cycle ; la fonction
passera par un maximum, c’est-à-dire que pour une certaine valeur de à laquelle correspondent les valeurs et de et , on aura :
c’est à dire que quand est égal à et que l’on fait varier depuis jusqu’à , la fonction passe par un maximum ou un minimum, ou que :
C.Q.F.D.
Résolution du 2e problème
Pour démontrer qu’une région douteuse est monocyclique ou acyclique, il suffit donc de faire voir que l’on peut trouver deux fonctions et satisfaisant aux conditions de l’énoncé du théorème précédent et telles que l’on n’ait en aucun point de la région
Suite de la discussion
Si le système topographique :
ne suffit pas pour obtenir une séparation complète des cycles limites, on considérera un nombre aussi grand qu’on voudra de systèmes satisfaisant aux mêmes conditions :
1° Il est clair que chacun de ces systèmes fournis sont de nouveaux cycles sans contact, certaines portions des régions douteuses laissées par le système seront sillonnées par ces cycles et deviendront acycliques.
2° Parmi les régions douteuses laissées par l’ensemble de tous ces systèmes il y en aura dans l’intérieur desquelles il sera impossible de faire passer un cycle entourant l’origine; ces régions seront donc aussi acycliques (voir l’exemple II au chapitre suivant).
3° Les régions douteuses devenant de plus en plus restreintes, finiront en général par devenir toutes acycliques ou monocyclique, de manière à achever la séparation des cycles limites; cette séparation sera même toujours possible; et quand on n’aura pas deux cycles limites confondus, on pourra toujours s’apercevoir qu’elle est terminée.
4° Les régions cycliques devenant de plus en plus restreintes, on connaîtra le cycle limite avec une approximation aussi grande que l’on voudra.
Remarque
La théorie de la séparation des cycles limites présente quelque analogie avec les procédés qui servent à séparer les racines d’une équation algébrique.
A ce point de vue, la manière dont se résout le premier problème rappelle la méthode des substitutions
qui permet de reconnaître, si, dans un intervalle donné, une équation algébrique admet un nombre pair ou impair de racines.
Le théorème XIX est l’équivalent du théorème de Rolle.
Quant au cas des cycles limites confondus, qui correspond à celui des racines multiples, il présente certaine difficultés spéciales que je n’ai pas encore résolues.
Chapitre IX : Exemples de discussions incomplètes
Exemple I
Soit l’équation différentielle :
qui en posant
devient
Prenons pour le système topographique , le système des cercles
La courbe des contacts de ces cercles se réduit à l’ellipse sphérique :
qui enveloppe l’origine. Par conséquent, les régions :
sont acycliques; pendant que la région :
est douteuse; mais si l’on observe que les cycles , ; sont de signe contraire; on verra qu’elle est cyclique.
Appuyons-nous maintenant sur le théorème XIX en faisant
d’où :
La courbe est une ellipse sphérique passant par l’origine et tangente au cercle . Donc en aucun point de la région ; on a :9090endnote: 90 “” devient “” dans la version imprimée.
Donc cette région est monocyclique.
Conséquences
Outre l’équateur, il y a un cycle limite dans chaque hémisphère et un seul; ce cycle est tout entier dans la région .
Si un point mobile se meut suivant la loi suivante ( étant le temps),
Si pour ; on a ; le mobile sortira certainement du cercle et il ne sortira certainement pas du cercle .
Exemple II
Soit l’équation :
d’où
Considérons encore les cercles ; nous verrons que les
régions , sont acycliques pendant que la région est douteuse.
Seulement ici les cycles , sont de même signe, de sorte que l’on ne peut affirmer que cette région soit cyclique.
Considérons le cycle :
Pour qu’il eût un contact, il faudrai que l’on eût :
| () |
Mais tout le long du cycle , on a :
et
La relation ne peut donc être satisfaite, c’est à dire que le cycle est sans contact. Il en sera de même des cycles pourvu que , et que est suffisamment petit.
La région est donc acyclique. Il resterait donc deux régions douteuses :
1° La région ,
2° La région ,
Mais dans aucune de ces régions on ne peut faire passer de cycle enveloppant l’origine. Elles sont donc aussi acycliques.
Conséquences
Il n’y a pas d’autre cycle limite que l’équateur.
Un point mobile se mouvant suivant la loi :
peut se rapprocher indéfiniment de l’équateur.
Exemple III
Soit l’équation :
La considération des cycles nous montre :
1° que les régions et sont acycliques.
2° que la région est douteuse.
De plus les cycles et étant de même signe, il doit y avoir dans cette région un nombre pair de cycles limites :
Considérons le cycle :
Ce cycle est tout entier dans la région douteuse; il est sans contact; ainsi que les cycles :
et où est très petit. De plus ces cycles ne sont pas de même signe que les cycles et .
Nous avons donc les régions suivantes :
| 1ère région | Acyclique. | |
| 2e région | , | Cyclique. |
| 3e région | , | Acyclique. |
| 4e région | , | Cyclique. |
| 5e région | Acyclique. |
Appliquons maintenant le théorème XIX, en faisant :
où9191endnote: 91 “” devient “” dans la version imprimée.
La courbe 9292endnote: 92 Voir note précédente. se réduit donc aux deux cycles
qui sont tout entiers l’un dans la 1ère, l’autre dans la 3e région. Comme d’ailleurs ni , ni ne deviennent infini, la 2e et la 4e régions sont monocycliques.
Conclusion
En dehors de l’équateur, il y a dans chaque hémisphère deux cycles limites et il n’y en a que deux.
AD 53p. Private collection, Paris 75017.
Notes
- 1 Le manuscrit porte une note marginale de main inconnue: “16 Belouze”.
- 2 Variante : “nous conviendrons, pour finir les idées, de suivre…”.
- 3 Variante : “Par exemple, un point nous considérerons…”
- 4 Variante : “ et ou ”.
- 5 Variante : “(figure 2 6)”.
- 6 Variante : “comme et non pas …”.
- 7 “continues” a été enlevé dans la version imprimée.
- 8 Variante : “(figure 3 7)”.
- 9 Variante : “…sans s’en éloigner …”.
- 10 Variante : “(figure 4 8)”.
- 11 “demi” a été rajouté entre “Cette” et “caractéristique”.
- 12 “en partant du point ” a été rajouté entre “Si” et ”au lieu de considérer”.
- 13 Variante : “…celle de droite, et qu’on fût arrivé on aurait …”.
- 14 Variante : “(figure 5 9)”.
- 15 Note présente dans la marge : “Note pour l’imprimeur : Sur l’arc les points se succèdent dans l’ordre suivant : ”.
- 16 Variante : “L’arc Le cycle …”.
- 17 Variante : “…S’il rencontre se confond …”.
- 18 La virgule a été remplacé par un point virgule.
- 19 Variante : “…s’il a un conséquent , si et sont les valeurs de qui correspondent à et à si …”.
- 20 a été corrigé par dans la version imprimée.
- 21 Variante : “Soit En effet …”.
- 22 Variante : “En effet nous supposons avons supposé que …”.
- 23 Variante : “…une surface qui coupe le cylindre qui a pour base le passe par …”.
- 24 Variante : “…correspondent à des cols caractéristiques …”.
- 25 Variante : “Si l’on divise l’arc sans contact en a Si les extrémités de l’arc sans contact …”.
- 26 Variante : “…à une valeur donnée quelconque de …”.
- 27 Variante : “(figure 6 10)”.
- 28 Une virgule a été ajouté ici dans la version imprimée.
- 29 Variante : “…aux axes; les points en suivant …”.
- 30 Variante : “…la courbe dans un certain sens …”.
- 31 Variante : “(figure 7 11)”.
- 32 ”présentera” devient ”représentera” dans la version imprimée.
- 33 La version imprimée commence par une suppostion : “Supposons qu’à certaines valeurs …”.
- 34 “Aux valeurs” devient “Que de plus aux valeurs” dans la version imprimée.
- 35 Variante : “Nous supposerons d’abord que les branches de courbe De tous les cols…”.
- 36 Il manque ici quatre pages (de la page 74 à la page 77 du manuscrit); ces pages correspondent à la fin du Chapitre V de la version imprimée, pages 259 à 261, comprenant quatre figures numérotées 12 à 15.
- 37 Variante : “De mem D’après”.
- 38 Variante : “(figure 12 6)”.
- 39 une virgule a été ajouté dans la version imprimée.
- 40 une virgule a été ajouté dans la version imprimée.
- 41 Variante : ”On pourra prendre assez grand po Soit ”.
- 42 Variante : “…,…, de telle et que …”.
- 43 Variante : “(figure 13 7)”.
- 44 Variante : “(figure 14 8)”.
- 45 La virgule n’apparaît pas dans la version imprimée.
- 46 Variante : “(figure 15 9)”.
- 47 Variante : “ ”.
- 48 Variante : “…et de celui ci ensuite par une cycle série infiniment …”.
- 49 Variante : “y ”.
- 50 Variante : “…si deux des tangencs venant viennent à se …”.
- 51 Variante : “…des points , ; mais si l’on suppose nous supposerons : 1° que les points …”.
- 52 “” devient “” dans la version imprimée.
- 53 Variante : “…sautera de à + …”.
- 54 Variante : “…le premier hémisphère, et de + ”.
- 55 Variante : “(figure 16 20)”.
- 56 Variante : “…”.
- 57 ”, , , ” devient ”, , , , ” dans la version imprimée.
- 58 Variante : “…soit et et ….”.
- 59 Variante : “…on trouvera toujours sur l’équateur la sphère …”.
- 60 Variante : “…d’un changement linéaire de variable …”.
- 61 Variante : “…Si l’on ne trouve pas sur l’équateur la sphère …”.
- 62 Variante : “…c’est que le cycle passe par deux points les points du cycle sont deux à deux …”.
- 63 Variante : “…c’est à dire qu’il que le cycle est …”.
- 64 Variante : “En effet Soient :…”.
- 65 Une note est présente dans la marge : “1b (ou 16) Brabant”.
- 66 Variante : “On peut le diviser en y découper un certain …”.
- 67 Variante : “…la loi de conséquence de cet arc l’un de ces arcs, …”.
- 68 Variante : “…Supposons que l’on représente par considère le point …”.
- 69 “” devient “” dans la version imprimée.
- 70 Variante : “(figure 17 21)”.
- 71 Variante : “…par un point deu l’ar segment …”.
- 72 “” devient “” dans la version imprimée.
- 73 Variante : “…joindre par des droites, et , et , puis …”.
- 74 Variante : “…cycle limite ne passait par un noeud col, car nous …”.
- 75 Variante : “…Une pareil cycle caractéristique n’est limite cycle limite …”.
- 76 Variante : “(figure 18 22)”.
- 77 La forme de la figure est différente dans la version imprimée, cette dernière ayant une forme arrondie à la place d’une forme en huit.
- 78 Variante : “(figure 19 23)”.
- 79 Le manuscrit comporte une note marginale en crayon de couleur bleue de main inconnue, sans doute du compositeur: “ital”, accompagnée d’une accolade sur le côté du théorème.
- 80 Une note marginale de la main de Poincaré accompagne la figure: “Voir les figures 21, 22, 23, 24 à plus grande échelle aux pages 103, 104 et 105”. Il s’agit, après une opération de rénumeration réalisée sans doute par Poincaré des figures 25 à 28.
- 81 Variante barrée: “ ”.
- 82 La légende est adaptée à la figure de la transcription (les figures à grandes échelles sont légèrement différentes de celles illustrant les exemples). Dans le manuscrit, les deux cycles limites sont indiqués dans la figure 26 par deux cercles dont la circonférence est hachée. La figure du manuscrit n’est pas colorée.
- 83 Une erreur est présente dans la version imprimée, il est écrit “” au lieu de “”.
- 84 Les pages suivantes du manuscrit (page 103 à 105) sont consacrées aux représentations à plus grandes échelles des figures 25 à 28. Une note est écrite à côté de la figure 28 : “Manque la fig 28 (petite échelle)”.
- 85 Ce 1\uper problème était présenté d’abord comme le 2\upe problème (cette mention étant barrée). Aux pages 109–110 du manuscrit se trouve ce que Poincaré presentait d’abord comme le 1\uper problème; nous le transcrivons ainsi : “1\uper Problème : Reconnaître si une région douteuse est cyclique. Supposons que l’un des cycles qui forment la courbe des contacts entoure l’origine et soit situé tout entier dans une région douteuse, je dis que cette région est cyclique.En effet envisageons le système topographique des cycles sans contact et des cycles limites, système topographique dont le théorème XVIII a démontré l’existence, et envisageons le lieu des points de contact des cycles de ce système avec les cycles ; ce lieu est une courbe continue qui passe par l’origine et va couper l’équateur. Aux points où elle coupe la courbe il y a contact entre une caractéristique et l’un des cycles ; ce cycle n’est donc pas sans contact, c’est donc un cycle limite. Mais si un des cycles M1 qui forment cycle faisant partie de la courbe entoure l’origine, il sera forcément coupé par la courbe qui va de l’origine à l’équateur; et par conséquent par un cycle limite; si donc il est tout entier dans une région douteuse cette région sera cyclique. C.Q.F.D. 2\upe Problème. Reconnaître si une région cyclique est monocyclique.”
- 86 Une note est présente dans la marge :“Rochereau”.
- 87 “” devient “” dans la version imprimée.
- 88 Le manuscrit porte un note marginale de main inconnue : “Brabant”.
- 89 “” devient “” dans la version imprimée.
- 90 “” devient “” dans la version imprimée.
- 91 “” devient “” dans la version imprimée.
- 92 Voir note précédente.
Références
- Mémoire sur les courbes définies par une équation différentielle (2nde partie). Journal de mathématiques pures et appliquées 8, pp. 251–296. External Links: Link Cited by: Mémoire sur les courbes définies par une équation différentielle.
Time-stamp: "29.10.2023 21:23"